Advertisements
Advertisements
Question
A boy standing at a point O finds his kite flying at a point P with distance OP = 25 m. It is at a height of 5 m from the ground. When the thread is extended by 10 m from P, it reaches a point Q. What will be the height QN of the kite from the ground? (use trigonometric ratios)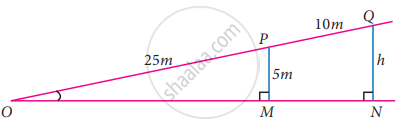
Solution
Let the angle O be “θ”
In ΔONQ
sin θ = `"opposite side"/"hypotenuse" = "QN"/"OQ"`
sin θ = `"h"/((25 + 10))`
= `"h"/35` ...(1)
In ΔOMP
sin θ = `"PM"/"OP"`
⇒ sin θ = `5/25`
sin θ = `1/5` ...(2)
From (1) and (2) we get
`"h"/35 = 1/5`
5h = 35
⇒ h = `35/5`
= 7
The height of the kite from the ground is 7m.
APPEARS IN
RELATED QUESTIONS
If 3cos θ – 4sin = 2cos θ + sin θ Find tan θ.
If sin θ = `3/4` show that `sqrt((cosec^2theta - cot^2theta)/(sec^2theta-1)) =sqrt(7)/3`
If cos θ = `3/5` , show that `((sin theta - cot theta ))/(2tan theta)=3/160`
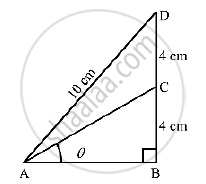
In the adjoining figure, `∠B = 90° , ∠BAC = theta° , BC = CD = 4cm and AD = 10 cm`. find (i) sin theta and (ii) `costheta`
Evaluate:
cos450 cos300 + sin450 sin300
Using the formula, tan 2A =`(2 tan A )/(1- tan^2 A)` find the value of tan 600, it being given that tan 300 = `1/sqrt(3)`.
If sin (A + B) = 1 and cos (A – B) = 1, 00 ≤ (A + B) ≤ 900 and A > B, then find A and B.
tan 30° × tan ______° = 1
From the following figure, find the values of :
(i) sin A
(ii) sec A
(iii) cos2 A + sin2A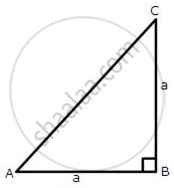
If 2 cos θ = `sqrt(3)`, then find all the trigonometric ratios of angle θ
