Advertisements
Advertisements
Question
If cos θ = `3/5` , show that `((sin theta - cot theta ))/(2tan theta)=3/160`
Solution
LHS = `((sin theta - cot theta ))/(2tantheta)`
=`(sin theta costheta /sintheta )/(2(sintheta/costheta))`
=`((sin^2theta - costheta)/sintheta)/((2 sintheta/costheta))`
=` (costheta(sin^2theta-costheta))/(2sin^2theta)`
=`(costheta (1-cos^2theta-costheta))/(2(1-cos^2theta))`
=`(3/5[1-(3/5)^2-3/5])/(2[1-(3/5)^2])`
=`(3/5(1/1-9/25-3/5))/(2(1-9/25))`
=`(3/5((25-9-15)/25))/(2((25-9)/25))`
=`(3/5(1/25))/(2(16/25))`
=`3/(5xx2xx16)`
=`3/160`
= RHS
APPEARS IN
RELATED QUESTIONS
if `sec theta = 5/4` find the value of `(sin theta - 2 cos theta)/(tan theta - cot theta)`
If tan `theta = a/b`, show that `((a sin theta - b cos theta))/((a sin theta + bcos theta))= ((a^2-b^2))/(a^2+b^2)`
Given: cos A = 0.6; find all other trigonometrical ratios for angle A.
If cot θ= 1; find the value of: 5 tan2 θ+ 2 sin2 θ- 3
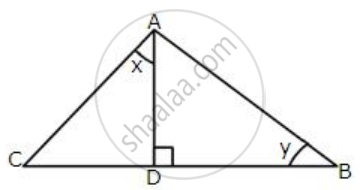
In the following figure:
AD ⊥ BC, AC = 26 CD = 10, BC = 42, ∠DAC = x and ∠B = y.
Find the value of :
(i) cot x
(ii) `1/sin^2 y – 1/tan^2 y`
(iii) `6/cos x – 5/cos y + 8 tan y`.
If sin A = cos A, find the value of 2 tan2A - 2 sec2 A + 5.
If sec A = `sqrt2` , find : `(3cot^2 "A"+ 2 sin^2 "A")/ (tan^2 "A" – cos ^2 "A")`.
If 8 tanθ = 15, find (i) sinθ, (ii) cotθ, (iii) sin2θ - cot2θ
If sin A = `(7)/(25)`, find the value of : `"cos A" + (1)/"cot A"`
If 2 cos θ = `sqrt(3)`, then find all the trigonometric ratios of angle θ
