Advertisements
Advertisements
Question
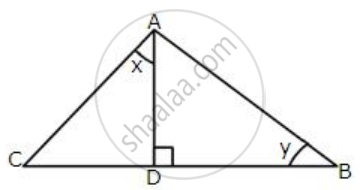
In the following figure:
AD ⊥ BC, AC = 26 CD = 10, BC = 42, ∠DAC = x and ∠B = y.
Find the value of :
(i) cot x
(ii) `1/sin^2 y – 1/tan^2 y`
(iii) `6/cos x – 5/cos y + 8 tan y`.
Solution
Given the angle, DAC = 90° and ∠ADB = 90° in the figure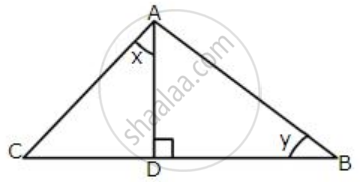
⇒ AC2 = AD2 + DC2 ...(AC is hypotenuse in ΔADC)
⇒ AD2 = AC2 - DC2
⇒ AD2 = 262 – 102
∴ AD2 = 576
∴ AD2 = `sqrt(576)`
∴ AD = 24
Again, In ΔABD
⇒ AB2 = AD2 + BD2 ...(AB is hypotenuse in ΔABD)
⇒ AB2 = 242 + 322
⇒ AB2 = 576 + 1024
⇒ AB2 = `sqrt1600`
∴ AB = 40
Now
(i) cot x = `"base"/"perpendicular" = "AD"/"CD" = (24)/(10) = 2. 4`
(ii) sin y = `"perpendicular"/"hypotenuse" ="AD"/"AB" = (24)/(40) = (3)/(5)`
tan y = `"perpendicular"/"base" ="AD"/"BD" = (24)/(32) = (3)/(4)`
Therefore
`1/sin^2 y – 1/tan^2 y`
= `1/(3/5)^2 – 1/(3/4)^2`
= `(5/3)^2 - (4/3)^2`
= `(25)/(9) – (16)/(9)`
= `(9)/(9)`
= 1
(iii) tan y =`"perpendicular"/"base" = "AD"/"BD" = (24)/(32) = (3)/(4)`
cos x = `"base"/"hypotenuse" = "AD"/"AC" = (24)/(26) = (12)/(13)`
cos y = `"base"/"hypotenuse" = "BD"/"AB" = (32)/(40) = (4)/(5)`
Therefore
`6/ cos x – 5/ cos y + 8tan y`
= `6/(12/13) – 5/(4/5) + 8(3/4)`
= `(13)/(2) – (25)/(4) + 6`
= `(26 – 25 + 24)/(4)`
= `(25)/(4)`
= `6(1)/(4)`
APPEARS IN
RELATED QUESTIONS
If 3cos θ – 4sin = 2cos θ + sin θ Find tan θ.
In ∆PQR, right-angled at Q, PQ = 3 cm and PR = 6 cm. Determine ∠P and ∠R.
If cos θ = `7/25` find the value of all T-ratios of θ .
Verify each of the following:
(ii)`cos 60^0 cos 30^0+ sin 60^0 sin30^0`
If A = 450 , verify that:
(ii) cos 2A = 2 cos2 A – 1 = 1 – 2 sin2 A
If sin A = cos A, find the value of 2 tan2A - 2 sec2 A + 5.
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
tan C = `(5)/(12)`
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
cosec C = `sqrt(10)`
In ΔABC, ∠B = 90°. If AB = 12units and BC = 5units, find: cot C
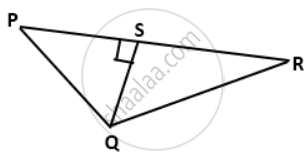
In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: sin P