Advertisements
Advertisements
Question
From the following figure, find:
(i) y
(ii) sin x°
(iii) (sec x° - tan x°) (sec x° + tan x°)

Solution
Consider the given figure :

(i) Since the triangle is a right-angled triangle, so using Pythagorean Theorem
22 = y2 + 12
y2 = 4 – 1 = 3
y = `sqrt3`
(ii) sin x° = `"perpendicular"/"hypotenuse" = (sqrt3)/(2)`
(iii) tan x° = `"perpendicular"/"base" = sqrt3`
sec x° = `"hypotenuse"/"base" = 2`
Therefore
( sec x° – tan x°) ( sec x° + tan x°)
= (2–`sqrt3`) (2+`sqrt3`)
= 4 – 3
= 1
APPEARS IN
RELATED QUESTIONS
if `sec A = 5/4` verify that `(3 sin A - 4 sin^3 A)/(4 cos^3 A - 3 cos A) = (3 tan A - tan^3 A)/(1- 3 tan^2 A)`
If sin θ = `3/4` show that `sqrt((cosec^2theta - cot^2theta)/(sec^2theta-1)) =sqrt(7)/3`
If x = cosec A +cos A and y = cosec A – cos A then prove that `(2/(x+y))^2 + ((x-y)/2)^2` = 1
Using the formula, cos A = `sqrt((1+cos2A)/2) ,`find the value of cos 300, it being given that cos 600 = `1/2`.
Given: tan A = `4/3 , "find" : ("cosec""A")/(cot "A"– sec "A")`
Using the measurements given in the following figure:
(i) Find the value of sin θ and tan θ.
(ii) Write an expression for AD in terms of θ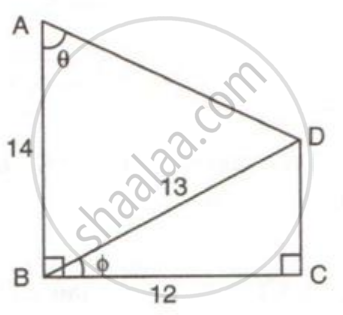
Given : 17 cos θ = 15;
Find the value of: tan θ + 2 secθ .
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
tan C = `(5)/(12)`
In a right-angled triangle PQR, ∠PQR = 90°, QS ⊥ PR and tan R =`(5)/(12)`, find the value of sin ∠PQS
If cosec θ = `(29)/(20)`, find the value of: `("sec" θ)/("tan" θ - "cosec" θ)`
