Advertisements
Advertisements
Question
In a right-angled triangle PQR, ∠PQR = 90°, QS ⊥ PR and tan R =`(5)/(12)`, find the value of sin ∠PQS
Solution
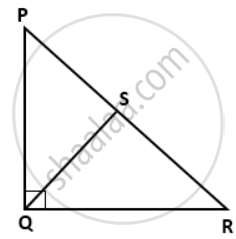
tan R = `(5)/(12)`
⇒ `"PQ"/"QR" = (5)/(12)`
⇒ PQ = 5 and QR = 12
In right-angled ΔPQR,
PR
= PQ2 + QR2
= 52 + 122
= 25 + 144
= 169
⇒ PR = 13
∠PQS + ∠P = 90° and ∠P + ∠R = 90°
⇒ ∠PQS + ∠P = ∠P +∠R
⇒ ∠PQS = ∠R
∴ sin ∠PQS
= sin R
= `"PQ"/"PR"`
= `(5)/(13)`.
APPEARS IN
RELATED QUESTIONS
If 8 tan A = 15, find sin A – cos A.
If tan θ = `1/sqrt(7) `show that ` (cosec ^2 θ - sec^2 θ)/(cosec^2 θ + sec^2 θ ) = 3/4`
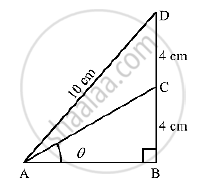
In the adjoining figure, `∠B = 90° , ∠BAC = theta° , BC = CD = 4cm and AD = 10 cm`. find (i) sin theta and (ii) `costheta`
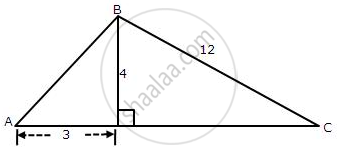
From the following figure, find the values of
(i) cos A
(ii) cosec A
(iii) tan2A - sec2A
(iv) sin C
(v) sec C
(vi) cot2 C - ` 1 / sin^2 "c"`
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
cos A = `(7)/(25)`
In an isosceles triangle ABC, AB = BC = 6 cm and ∠B = 90°. Find the values of cos2 C + cosec2 C
In the given figure, AD is the median on BC from A. If AD = 8 cm and BC = 12 cm, find the value of cos y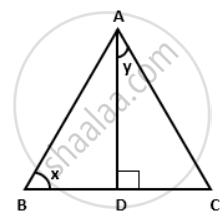
If sin A = `(7)/(25)`, find the value of : `(2"tanA")/"cot A - sin A"`
In the given figure, AC = 13cm, BC = 12 cm and ∠B = 90°. Without using tables, find the values of: sin A cos A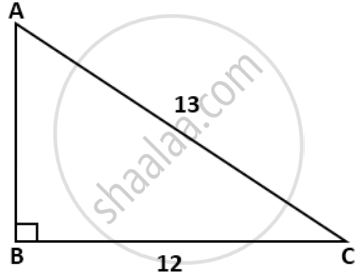
If cos θ : sin θ = 1 : 2, then find the value of `(8costheta - 2sintheta)/(4costheta + 2sintheta`
