Advertisements
Advertisements
Question
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
cos A = `(7)/(25)`
Solution
cos A = `(7)/(25)`
cosA = `"Base"/"Hypotenuse" = (7)/(25)`
By Pythagoras theorem, we have
(Hypotenuse)2 = (Perpendicular)2 + (Base)2
⇒ Perpendicular = `sqrt(("Hypotenuse")^2 - ("Base")^2`
⇒ Perpendicular
= `sqrt((25)^2 - (7)^2`
= `sqrt(625 - 49)`
= `sqrt(576)`
= 24
sinA = `"Perpendicular"/"Hypotenuse" = (24)/(25)`
tanA = `"Perpendicular"/"Base" = (24)/(7)`
secA = `(1)/"cosA" = (25)/(7)`
cotA = `(1)/"tanA" = (7)/(24)`
cosecA = `(1)/"sinA" = (25)/(24)`.
APPEARS IN
RELATED QUESTIONS
Given 15 cot A = 8. Find sin A and sec A.
If ∠A and ∠B are acute angles such that tan A= Tan B then prove that ∠A = ∠B
Verify each of the following:
(iii) `2 sin 30^0 cos 30^0`
sin20° = cos ______°
Form the following figure, find the values of:
- cos B
- tan C
- sin2B + cos2B
- sin B. cos C + cos B. sin C

Given: sin θ = `p/q`.
Find cos θ + sin θ in terms of p and q.
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
cosB = `(4)/(5)`
In a right-angled triangle PQR, ∠PQR = 90°, QS ⊥ PR and tan R =`(5)/(12)`, find the value of tan ∠SQR
If cosec θ = `(29)/(20)`, find the value of: cosec θ - `(1)/("cot" θ)`
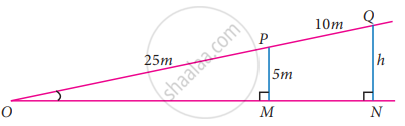
A boy standing at a point O finds his kite flying at a point P with distance OP = 25 m. It is at a height of 5 m from the ground. When the thread is extended by 10 m from P, it reaches a point Q. What will be the height QN of the kite from the ground? (use trigonometric ratios)