Advertisements
Advertisements
Question
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
sinB = `sqrt(3)/(2)`
Solution
sinB = `sqrt(3)/(2)`
sinB = `"Perpendicular"/"Hypotenuse" = sqrt(3)/(2)`
By Pythagoras theorem, we have
(Hypotenuse)2 = (Perpendicular)2 + (Base)2
⇒ Base = `sqrt(("Hypotenuse")^2 - ("Perpendicular")^2`
⇒ Base
`sqrt((2)^2 - (sqrt(3))^2`
= `sqrt(4 - 3)`
= `sqrt(1)`
= 1
cosB = `"Base"/"Hypotenuse" = (1)/(2)`
tanB = `"Perpendicular"/"Base" = sqrt(3)`
secB = `(1)/"cosB"` = 2
cotB = `(1)/"tanB" = (1)/sqrt(3)`
cosecB= `(1)/"sinA" = (2)/sqrt(3)`.
APPEARS IN
RELATED QUESTIONS
Given 15 cot A = 8. Find sin A and sec A.
If A = B = 60°. Verify `tan (A - B) = (tan A - tan B)/(1 + tan tan B)`
Evaluate:
`(sin30°)/(cos 45°)+(cot45°)/(sec60° )- (sin60°)/(tan45°)+(cos30°)/(sin90°)`
If A and B are acute angles such that tan A =`1/3, tan B = 1/2 and tan (A + B) =` show that `A+B = 45^0`
Given: sin θ = `p/q`.
Find cos θ + sin θ in terms of p and q.
If sec A = `sqrt2`, find the value of :
`(3cos^2"A"+5tan^2"A")/(4tan^4"A"–sin^2"A")`
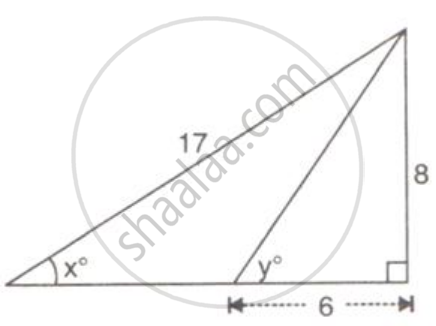
Use the given figure to find :
(i) sin xo
(ii) cos yo
(iii) 3 tan xo - 2 sin yo + 4 cos yo.
In triangle ABC, AB = AC = 15 cm and BC = 18 cm. Find:
- cos B
- sin C
- tan2 B - sec2 B + 2
If cosB = `(1)/(3)` and ∠C = 90°, find sin A, and B and cot A.
If cosec θ = `(29)/(20)`, find the value of: `("sec" θ)/("tan" θ - "cosec" θ)`
