Advertisements
Advertisements
Question
If A = 450 , verify that:
(ii) cos 2A = 2 cos2 A – 1 = 1 – 2 sin2 A
Solution
A= 450
`⇒ 2A = 2xx45^0=90^0`
(ii) cos 2 A = cos `90^0 = 0`
`2 cos^2 -1 = 2 cos ^2 45 ^0-1 = 2 xx(1/sqrt(2))^2 -1=2 xx1/2 -=1-1=0`
Now , `1-2 sin^2 A =1-2 xx(1/sqrt(2)^2 )-1=1-2xx1/2=1-1=0`
∴ cos 2A = 2 cos2 A – 1 = 1 – 2 sin2 A
APPEARS IN
RELATED QUESTIONS
In right angled triangle ΔABC at B, ∠A = ∠C. Find the values of Sin A cos C + Cos A Sin C
If A and B are acute angles such that tan A = 1/2, tan B = 1/3 and tan (A + B) = `(tan A + tan B)/(1- tan A tan B)` A + B = ?
If cos 2θ = sin 4θ where 2θ, 4θ are acute angles, find the value of θ.
In ΔABC , ∠C = 90° ∠ABC = θ° BC = 21 units . and AB= 29 units. Show thaT `(cos^2 theta - sin^2 theta)=41/841`
Evaluate:
cos450 cos300 + sin450 sin300
If sin (A+B) = sin A cos B + cos A sin B and cos (A-B) = cos A cos B + sin A sin B
(i) sin (750)
(ii) cos (150)
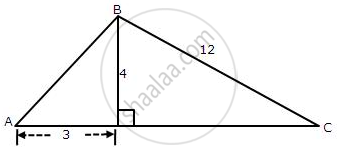
From the following figure, find the values of
(i) cos A
(ii) cosec A
(iii) tan2A - sec2A
(iv) sin C
(v) sec C
(vi) cot2 C - ` 1 / sin^2 "c"`
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
cotA = `(1)/(11)`
If sin θ = `(8)/(17)`, find the other five trigonometric ratios.
If cosec θ = `(29)/(20)`, find the value of: cosec θ - `(1)/("cot" θ)`
