Question

In ΔABC , ∠C = 90°  ∠ABC = θ°   BC = 21 units . and AB= 29 units. Show thaT `(cos^2 theta - sin^2 theta)=41/841`

Answer 1

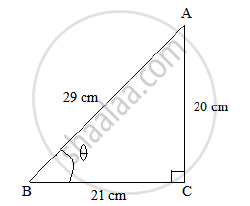
Using Pythagoras theorem, we get:
`AB^2 = AC^2 + BC^2`
`⟹ AC^2 = AB^2 − BC^2`
`⟹ AC^2 = (29)^2 − (21)^2`
`⟹ AC^2 = 841 − 441`
`⟹ AC^2 = 400`
⟹ 𝐴𝐶 = `sqrt(400)` = 20 𝑢𝑛𝑖𝑡𝑠

Now , sin `theta =(AC)/(AB) = (2theta)/29 and cos theta = (BC)/(AB)=21/29`

`cos^2 theta - sin^2 theta = (21/29)^2 - (20/29)^2 = 441/841 - 400/841 = 41/841`

Hence proved.