Advertisements
Advertisements
Question
In a ΔABC , ∠B = 90° , AB= 24 cm and BC = 7 cm find (i) sin A (ii) cos A (iii) sin C (iv) cos C
Solution
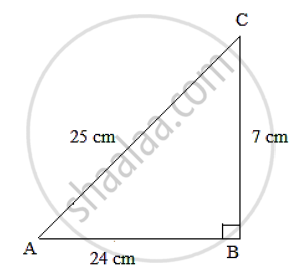
Using Pythagoras theorem, we get:
`AC^2 = AB^2 + BC^2`
`⟹ AC^2 = (24)^2 + (7)^2`
`⟹ AC^2 = 576 + 49 = 625`
⟹ 𝐴𝐶 = 25 𝑐𝑚
Now, for T-Ratios of ∠𝐴, 𝑏𝑎𝑠𝑒 = 𝐴𝐵 𝑎𝑛𝑑 𝑝𝑒𝑟𝑝𝑒𝑛𝑑𝑖𝑐𝑢𝑙𝑎𝑟 = 𝐵𝐶
(i) sin A = `(BC)/(AC) = 7/25`
(ii) cos A = `(AB)/(AC)=24/25`
Similarly, for T-Ratios of ∠𝐶, 𝑏𝑎𝑠𝑒 = 𝐵𝐶 𝑎𝑛𝑑 𝑝𝑒𝑟𝑝𝑒𝑛𝑑𝑖𝑐𝑢𝑙𝑎𝑟 = 𝐴𝐵
(iii) sin C = `(AB)/(AC)=24/25`
(iv) cos C= `(BC)/(AC)=7/25`
APPEARS IN
RELATED QUESTIONS
If cos 2θ = sin 4θ where 2θ, 4θ are acute angles, find the value of θ.
If x = cot A + cos A and y = cot A – cos A then prove that `((x-y)/(x+y))^2 + ((x-y)/2)^2=1`
Evaluate:
`4/(cot^2 30^0) +1/(sin^2 30^0) -2 cos^2 45^0 - sin^2 0^0`
Verify each of the following:
(iii) `2 sin 30^0 cos 30^0`
If sin (A + B) = 1 and cos (A – B) = 1, 00 ≤ (A + B) ≤ 900 and A > B, then find A and B.
If sin (A – B) = `1/2` and cos (A + B) = `1/2, 0^0 ≤ (A + B) ≤ 90^0` and A > B, then find A and B.
If 3x = cosecθ = and `3/x= cottheta` find the value of 3`(x^2-1/x^2)`.
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
tanB = `(8)/(15)`
In an isosceles triangle ABC, AB = BC = 6 cm and ∠B = 90°. Find the values of cos2 C + cosec2 C
If cosec θ = `(29)/(20)`, find the value of: `("sec" θ)/("tan" θ - "cosec" θ)`
