Advertisements
Advertisements
Question
If A = 600 and B = 300, verify that:
(i) sin (A + B) = sin A cos B + cos A sin B
Solution
A = 600 and B = 300
Now, A + B = 600 + 300 = 900
Also, A – B = 600 – 300 = 300
(i) sin (A + B) = sin 900 = 1
sin A cos B + cos A sin B = sin 600 cos 300 + cos 600 sin 300
=`(sqrt(3)/2xx sqrt(3)/2 + 1/2xx1/2) = (3/4+1/4)=1`
∴ sin (A + B) = sin A cos B + cos A sin B
APPEARS IN
RELATED QUESTIONS
If A = B = 60°, verify that cos (A − B) = cos A cos B + sin A sin B
If Sin (A + B) = 1 and cos (A – B) = 1, 0° < A + B ≤ 90° A ≥ B. Find A & B
If cosec θ= 2 show that `(cot θ +sin θ /(1+cos θ )) =2`
If tan θ = `20/21` show that `((1-sin θ + cos θ))/((1+ sin θ +cos θ)) = 3/7`
sin20° = cos ______°
Prove that
sin (50° + θ ) − cos (40° − θ) + tan 1° tan 10° tan 80° tan 89° = 1.
Using the measurements given in the following figure:
(i) Find the value of sin θ and tan θ.
(ii) Write an expression for AD in terms of θ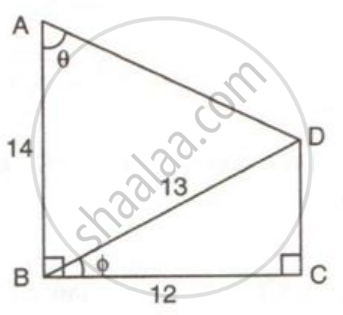
In the given figure;
BC = 15 cm and sin B = `(4)/(5)`
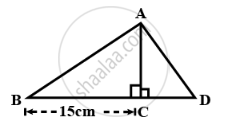
- Calculate the measure of AB and AC.
- Now, if tan ∠ADC = 1; calculate the measures of CD and AD.
Also, show that: tan2B - `1/cos^2 "B" = – 1 .`
If sin A + cosec A = 2;
Find the value of sin2 A + cosec2 A.
In the given figure, AD is the median on BC from A. If AD = 8 cm and BC = 12 cm, find the value of cos y