Advertisements
Advertisements
Question
In the given figure;
BC = 15 cm and sin B = `(4)/(5)`
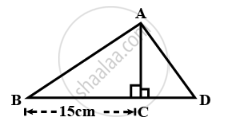
- Calculate the measure of AB and AC.
- Now, if tan ∠ADC = 1; calculate the measures of CD and AD.
Also, show that: tan2B - `1/cos^2 "B" = – 1 .`
Solution
Given
sin B = `(4)/(5)`
Now, sin B = `"P"/"H"`
`4/5 = "AC"/"AB"`
Therefore AC = 4x, and AB = 5x
Since
BC2 + AC2 = AB2 ...[ Using Pythagoras Theorem]
(5x)2 – (4x)2 = BC
BC2 = 9x2
∴ BC = 3x
Now
BC = 15
3x = 15
x = 5
(i) AC = 4x
= 4 x 5
= 20 cm
And
AB = 5x
= 5 x 5
= 25 cm
(ii) Given
tan ∠ADC = `(1)/(1)`
i.e. `"perpendicular"/"base" = "AC"/"CD" = (1)/(1)`
Therefore if length of perpendicular = x, length of hypotenuse = x
Since
AC2 + CD2 = AD2 ...[Using Pythagoras Theorem]
(x)2 – (x)2 = BC
AD2 = 2x2
∴ AD = `sqrt2x`
Now
AC = 20
x = 20
So
AD = `sqrt2x`
= `sqrt2` x 20
= 20`sqrt2"cm"`
And
CD = 20 cm
Now
tan B = `"AC"/"BC" = (20)/(15) = (4)/(3)`
cos B = `"BC"/"AB" = (15)/(25) = (3)/(5)`
So
tan2 B – `1/cos^2 B`
=`(4/3)^2 – 1/(3/5)^2`
= `(16)/(9) – (25)/(9)`
= `– (9)/(9)`
= – 1
APPEARS IN
RELATED QUESTIONS
if `cos theta = 5/13` find the value of `(sin^2 theta - cos^2 theta)/(2 sin theta cos theta) = 3/5`
`(cos 28°)/(sin 62°)` = ?
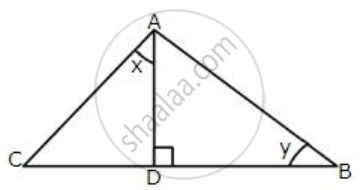
In the following figure:
AD ⊥ BC, AC = 26 CD = 10, BC = 42, ∠DAC = x and ∠B = y.
Find the value of :
(i) cot x
(ii) `1/sin^2 y – 1/tan^2 y`
(iii) `6/cos x – 5/cos y + 8 tan y`.
In the diagram, given below, triangle ABC is right-angled at B and BD is perpendicular to AC.
Find:
(i) cos ∠DBC
(ii) cot ∠DBA

In rhombus ABCD, diagonals AC and BD intersect each other at point O.
If cosine of angle CAB is 0.6 and OB = 8 cm, find the lengths of the side and the diagonals of the rhombus.
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
cosec C = `sqrt(10)`
In ΔABC, ∠A = 90°. If AB = 5 units and AC = 12 units, find: tan B.
In ΔABC, ∠B = 90°. If AB = 12units and BC = 5units, find: cot C
If sin A = `(7)/(25)`, find the value of : `"cos A" + (1)/"cot A"`
Evaluate: `5/(cot^2 30^circ) + 1/(sin^2 60^circ) - cot^2 45^circ + 2 sin^2 90^circ`.
