Advertisements
Advertisements
प्रश्न
In the given figure;
BC = 15 cm and sin B = `(4)/(5)`
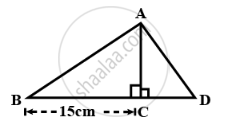
- Calculate the measure of AB and AC.
- Now, if tan ∠ADC = 1; calculate the measures of CD and AD.
Also, show that: tan2B - `1/cos^2 "B" = – 1 .`
उत्तर
Given
sin B = `(4)/(5)`
Now, sin B = `"P"/"H"`
`4/5 = "AC"/"AB"`
Therefore AC = 4x, and AB = 5x
Since
BC2 + AC2 = AB2 ...[ Using Pythagoras Theorem]
(5x)2 – (4x)2 = BC
BC2 = 9x2
∴ BC = 3x
Now
BC = 15
3x = 15
x = 5
(i) AC = 4x
= 4 x 5
= 20 cm
And
AB = 5x
= 5 x 5
= 25 cm
(ii) Given
tan ∠ADC = `(1)/(1)`
i.e. `"perpendicular"/"base" = "AC"/"CD" = (1)/(1)`
Therefore if length of perpendicular = x, length of hypotenuse = x
Since
AC2 + CD2 = AD2 ...[Using Pythagoras Theorem]
(x)2 – (x)2 = BC
AD2 = 2x2
∴ AD = `sqrt2x`
Now
AC = 20
x = 20
So
AD = `sqrt2x`
= `sqrt2` x 20
= 20`sqrt2"cm"`
And
CD = 20 cm
Now
tan B = `"AC"/"BC" = (20)/(15) = (4)/(3)`
cos B = `"BC"/"AB" = (15)/(25) = (3)/(5)`
So
tan2 B – `1/cos^2 B`
=`(4/3)^2 – 1/(3/5)^2`
= `(16)/(9) – (25)/(9)`
= `– (9)/(9)`
= – 1
APPEARS IN
संबंधित प्रश्न
if `sin theta = 3/5 " evaluate " (cos theta - 1/(tan theta))/(2 cot theta)`
If θ = 30° verify that `sin 2theta = (2 tan theta)/(1 + tan^2 theta)`
f θ = 30°, verify that cos 3θ = 4 cos3 θ − 3 cos θ
If cos θ = `7/25` find the value of all T-ratios of θ .
If sec θ = `5/4 ` show that `((sin θ - 2 cos θ))/(( tan θ - cot θ)) = 12/7`
If tan `theta = a/b`, show that `((a sin theta - b cos theta))/((a sin theta + bcos theta))= ((a^2-b^2))/(a^2+b^2)`
Verify each of the following:
(ii)`cos 60^0 cos 30^0+ sin 60^0 sin30^0`
If A = 300 , verify that:
(iii) tan 2A = `(2tanA)/(1-tan^2A)`
Given: tan A = `4/3 , "find" : ("cosec""A")/(cot "A"– sec "A")`
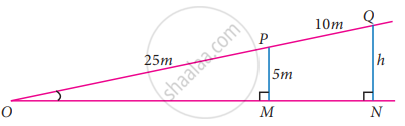
A boy standing at a point O finds his kite flying at a point P with distance OP = 25 m. It is at a height of 5 m from the ground. When the thread is extended by 10 m from P, it reaches a point Q. What will be the height QN of the kite from the ground? (use trigonometric ratios)