Advertisements
Advertisements
प्रश्न
A boy standing at a point O finds his kite flying at a point P with distance OP = 25 m. It is at a height of 5 m from the ground. When the thread is extended by 10 m from P, it reaches a point Q. What will be the height QN of the kite from the ground? (use trigonometric ratios)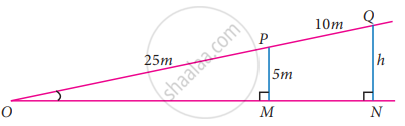
उत्तर
Let the angle O be “θ”
In ΔONQ
sin θ = `"opposite side"/"hypotenuse" = "QN"/"OQ"`
sin θ = `"h"/((25 + 10))`
= `"h"/35` ...(1)
In ΔOMP
sin θ = `"PM"/"OP"`
⇒ sin θ = `5/25`
sin θ = `1/5` ...(2)
From (1) and (2) we get
`"h"/35 = 1/5`
5h = 35
⇒ h = `35/5`
= 7
The height of the kite from the ground is 7m.
APPEARS IN
संबंधित प्रश्न
Find acute angles A & B, if sin (A + 2B) = `sqrt3/2 cos(A + 4B) = 0, A > B`
If sin θ = cos (θ – 45°), where θ – 45° are acute angles, find the degree measure of θ
If x = cot A + cos A and y = cot A – cos A then prove that `((x-y)/(x+y))^2 + ((x-y)/2)^2=1`
Verify each of the following:
(iii) `2 sin 30^0 cos 30^0`
If A = 300 , verify that:
(i) sin 2A = `(2 tan A)/(1+tan^2A)`
If A = 300 , verify that:
(iii) tan 2A = `(2tanA)/(1-tan^2A)`
Given : 5 cos A - 12 sin A = 0; evaluate:
`(sin "A"+cos"A")/(2 cos"A"– sin"A")`
In triangle ABC, AD is perpendicular to BC. sin B = 0.8, BD = 9 cm and tan C = 1.
Find the length of AB, AD, AC, and DC.
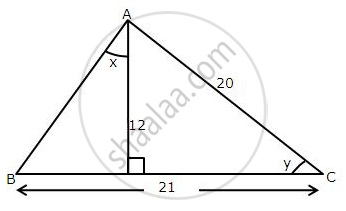
Use the information given in the following figure to evaluate:
`(10)/sin x + (6)/sin y – 6 cot y`.
If 5 cos θ = 3, evaluate : `(co secθ – cot θ)/(co secθ + cot θ)`
