Advertisements
Advertisements
प्रश्न
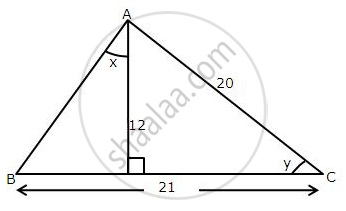
Use the information given in the following figure to evaluate:
`(10)/sin x + (6)/sin y – 6 cot y`.
उत्तर
In ΔADC, Using Pythagorean Theorem
AD2 + DC2 = AC2
DC2 = 202 – 122
DC2 = 256
DC = `sqrt(256)`
∴ DC = 16
Now,
BC = BD + DC
21 = BD + 16
∴ BD = 5
In ΔADB, using Pythagorean Theorem
AD2 + BD2 = AB2
122 + 52 = AB2
AB2 = 169
AB = `sqrt169`
∴ AB = 13
Now,
sin x = `"BD"/"AB" = (5)/(13)`
sin y = `"AD"/"AC" = (12)/(20) = (3)/(5)`
cot y = `"DC"/"AD" = (16)/(12) = (4)/(3)`
Therefore,
`(10)/sin x + (6)/sin y – 6 cot y`
`= (10)/(5/13) + (6)/(3/5) – 6 (4/3)`
`= 10 xx 13/5 + 6 xx 5/3 - 6(4/3)`
= `(130)/(5) + (30)/(3) – (24)/(3)`
= 26 + 10 – 8
= 28
APPEARS IN
संबंधित प्रश्न
If `sin (A – B) = 1/2` and `cos (A + B) = 1/2`, `0^@` < A + `B <= 90^@`, A > B Find A and B.
Find acute angles A & B, if sin (A + 2B) = `sqrt3/2 cos(A + 4B) = 0, A > B`
If sin θ = cos (θ – 45°), where θ – 45° are acute angles, find the degree measure of θ
If sin θ ,` sqrt (3)/2` find the value of all T- ratios of θ .
If sec `theta = 17/8 ` verify that `((3-4sin^2theta)/(4 cos^2theta -3))=((3-tan^2theta)/(1-tan^2theta))`
Given: cos A = 0.6; find all other trigonometrical ratios for angle A.
In an isosceles triangle ABC, AB = BC = 6 cm and ∠B = 90°. Find the values of cos C
In the given figure, AD is the median on BC from A. If AD = 8 cm and BC = 12 cm, find the value of cos y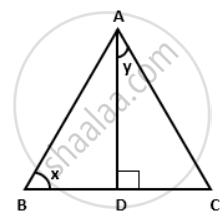
If 2 cos θ = `sqrt(3)`, then find all the trigonometric ratios of angle θ
If sin θ = `"a"/sqrt("a"^2 + "b"^2)`, then show that b sin θ = a cos θ
