Advertisements
Advertisements
Question
If A = 300 , verify that:
(iii) tan 2A = `(2tanA)/(1-tan^2A)`
Solution
A = 300
⇒ 2A = 2 × 300 = 600
(iii) tan 2A = tan `60^0 = sqrt(3)`
`(2 tan A)/(1- tan^2 A) = (2 tan 30^0)/( 1-tan^2 30^0
)` = `(2xx(1/sqrt(3)))/(1-(1/sqrt(3))^2` = `((2/sqrt(3)))/(1-(1/3))` = `((2/sqrt(3)))/(2/3)` = `(2/sqrt(3))xx3/2 = sqrt(3)`
∴ tan 2A = `(2tanA)/(1-tan^2A)`
APPEARS IN
RELATED QUESTIONS
If 3cos θ – 4sin = 2cos θ + sin θ Find tan θ.
If tan θ =`15/ 8 `, find the values of all T-ratios of θ.
If sin (A – B) = `1/2` and cos (A + B) = `1/2, 0^0 ≤ (A + B) ≤ 90^0` and A > B, then find A and B.
Prove that
sin (50° + θ ) − cos (40° − θ) + tan 1° tan 10° tan 80° tan 89° = 1.
In rhombus ABCD, diagonals AC and BD intersect each other at point O.
If cosine of angle CAB is 0.6 and OB = 8 cm, find the lengths of the side and the diagonals of the rhombus.
In triangle ABC, AD is perpendicular to BC. sin B = 0.8, BD = 9 cm and tan C = 1.
Find the length of AB, AD, AC, and DC.
If sinA = `(3)/(5)`, find cosA and tanA.
In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: 4sin2R - `(1)/("tan"^2"P")`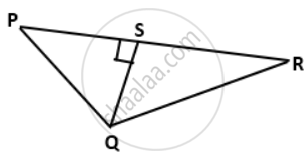
In an isosceles triangle ABC, AB = BC = 6 cm and ∠B = 90°. Find the values of cosec C
Assertion (A): For 0 < 0 ≤ 90°, cosec θ – cot θ and cosec θ + cot θ are reciprocal of each other.
Reason (R): cot2 θ – cosec2 θ = 1.
