Advertisements
Advertisements
प्रश्न
In ΔABC , ∠C = 90° ∠ABC = θ° BC = 21 units . and AB= 29 units. Show thaT `(cos^2 theta - sin^2 theta)=41/841`
उत्तर
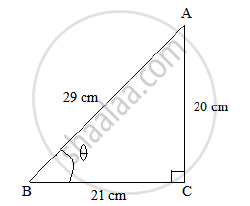
Using Pythagoras theorem, we get:
`AB^2 = AC^2 + BC^2`
`⟹ AC^2 = AB^2 − BC^2`
`⟹ AC^2 = (29)^2 − (21)^2`
`⟹ AC^2 = 841 − 441`
`⟹ AC^2 = 400`
⟹ 𝐴𝐶 = `sqrt(400)` = 20 𝑢𝑛𝑖𝑡𝑠
Now , sin `theta =(AC)/(AB) = (2theta)/29 and cos theta = (BC)/(AB)=21/29`
`cos^2 theta - sin^2 theta = (21/29)^2 - (20/29)^2 = 441/841 - 400/841 = 41/841`
Hence proved.
APPEARS IN
संबंधित प्रश्न
If 3 cot A = 4, Check whether `((1-tan^2 A)/(1+tan^2 A)) = cos^2 "A" - sin^2 "A"` or not.
In ∆PQR, right-angled at Q, PQ = 3 cm and PR = 6 cm. Determine ∠P and ∠R.
If sec 2A = cosec (A – 42°) where 2A is an acute angle. Find the value of A.
If ∠A and ∠B are acute angles such that tan A= Tan B then prove that ∠A = ∠B
Evaluate:
cos600 cos300− sin600 sin300
Prove that
cosec (65 °+ θ) sec (25° − θ) − tan (55° − θ) + cot (35° + θ) = 0
Given: sec A = `( 29 )/(21), "evaluate : sin A" - 1/tan "A"`
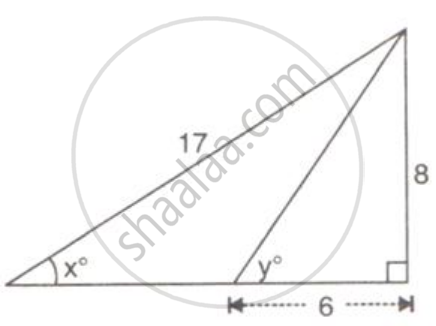
Use the given figure to find :
(i) sin xo
(ii) cos yo
(iii) 3 tan xo - 2 sin yo + 4 cos yo.
If cosB = `(1)/(3)` and ∠C = 90°, find sin A, and B and cot A.
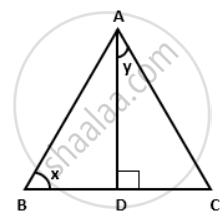
In the given figure, AD is the median on BC from A. If AD = 8 cm and BC = 12 cm, find the value of cos y