Advertisements
Advertisements
प्रश्न
In the given figure, AD is the median on BC from A. If AD = 8 cm and BC = 12 cm, find the value of cos y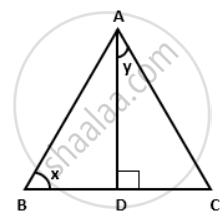
उत्तर

Since AD is median on BC, we have
BD = DC = `(1)/(2) xx "BC" = (1)/(2) xx 12` = 6cm
ΔADB is a right-angled triangle.
∴ AB2
= AD2 + BD2
= 82 + 62
= 64 + 36
= 100
⇒ AB = 10cm
ΔADC is a right-angled triangle.
∴ AC2
= AD2 + DC2
= 82 + 62
= 64 + 36
= 100
⇒ AC = 10cm
cos y
= `"AD"/"AC"`
= `(8)/(10)`
= `(4)/(5)`.
APPEARS IN
संबंधित प्रश्न
If x = cosec A +cos A and y = cosec A – cos A then prove that `(2/(x+y))^2 + ((x-y)/2)^2` = 1
Evaluate:
cos600 cos300− sin600 sin300
If A = 300 , verify that:
(ii) cos 2A = `(1- tan^2A)/(1+tan^2A)`
Given: sec A = `( 29 )/(21), "evaluate : sin A" - 1/tan "A"`
Using the measurements given in the following figure:
(i) Find the value of sin θ and tan θ.
(ii) Write an expression for AD in terms of θ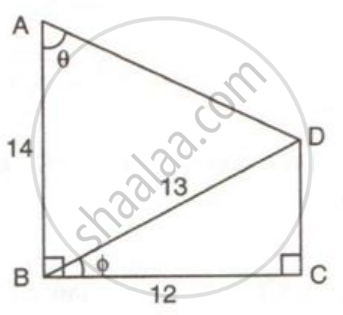
In the given figure; ∠C = 90o and D is mid-point of AC.
Find :
(i) `(tan∠CAB)/ (tan∠CDB)` (ii) `(tan∠ABC)/ (tan∠DBC)`
If 3 cos A = 4 sin A, find the value of :
(i) cos A(ii) 3 - cot2 A + cosec2A.
In ΔABC, ∠A = 90°. If AB = 5 units and AC = 12 units, find: sinB
If sin θ = `"a"/sqrt("a"^2 + "b"^2)`, then show that b sin θ = a cos θ
Assertion (A): For 0 < 0 ≤ 90°, cosec θ – cot θ and cosec θ + cot θ are reciprocal of each other.
Reason (R): cot2 θ – cosec2 θ = 1.
