Advertisements
Advertisements
Question
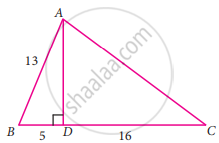
From the given figure, find the values of cos C
Solution
In the right ΔABD,
AD2 = AB2 – BD2
= 132 – 52
= 169 – 25
= 144
AD = `sqrt(144)`
= 12
In the right ΔADC,
AC2 = AD2 + DC2
= 122 + 162
= 144 + 256
= 400
AC = `sqrt(400)`
= 20
cos C = `"adjacent side"/"hypotenuse" = "CD"/"AC" = 16/20 = 4/5`
APPEARS IN
RELATED QUESTIONS
If sin θ = cos (θ – 45°), where θ – 45° are acute angles, find the degree measure of θ
If θ is a positive acute angle such that sec θ = cosec 60°, find 2 cos2 θ – 1
If sin θ = `a/b`, show that `(sectheta + tan theta) = sqrt((b+a)/(b-a))`
If ∠A and ∠B are acute angles such that tan A= Tan B then prove that ∠A = ∠B
If A and B are acute angles such that tan A =`1/3, tan B = 1/2 and tan (A + B) =` show that `A+B = 45^0`
In the given figure; ∠C = 90o and D is mid-point of AC.
Find :
(i) `(tan∠CAB)/ (tan∠CDB)` (ii) `(tan∠ABC)/ (tan∠DBC)`
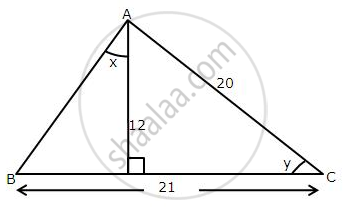
Use the information given in the following figure to evaluate:
`(10)/sin x + (6)/sin y – 6 cot y`.
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
sec B = `(15)/(12)`
If cosB = `(1)/(3)` and ∠C = 90°, find sin A, and B and cot A.
From the given figure, find the values of cosec C