Advertisements
Advertisements
प्रश्न
From the given figure, find the values of cos C
उत्तर
In the right ΔABD,
AD2 = AB2 – BD2
= 132 – 52
= 169 – 25
= 144
AD = `sqrt(144)`
= 12
In the right ΔADC,
AC2 = AD2 + DC2
= 122 + 162
= 144 + 256
= 400
AC = `sqrt(400)`
= 20
cos C = `"adjacent side"/"hypotenuse" = "CD"/"AC" = 16/20 = 4/5`
APPEARS IN
संबंधित प्रश्न
If `sin A = 9/41` compute cos 𝐴 𝑎𝑛𝑑 tan 𝐴
If cosec θ = `sqrt(10)` find all the values of all T-ratios of θ
If tan θ = `1/sqrt(7) `show that ` (cosec ^2 θ - sec^2 θ)/(cosec^2 θ + sec^2 θ ) = 3/4`
Evaluate:
`4/(cot^2 30^0) +1/(sin^2 30^0) -2 cos^2 45^0 - sin^2 0^0`
In the diagram, given below, triangle ABC is right-angled at B and BD is perpendicular to AC.
Find:
(i) cos ∠DBC
(ii) cot ∠DBA

If tan A + cot A = 5;
Find the value of tan2 A + cot2 A.
If sin A = cos A, find the value of 2 tan2A - 2 sec2 A + 5.
From the given figure, find the values of sec B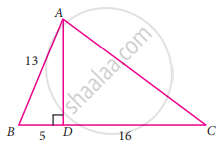
From the given figure, prove that θ + ∅ = 90°. Also prove that there are two other right angled triangles. Find sin α, cos β and tan ∅
Assertion (A): For 0 < 0 ≤ 90°, cosec θ – cot θ and cosec θ + cot θ are reciprocal of each other.
Reason (R): cot2 θ – cosec2 θ = 1.
