Advertisements
Advertisements
рдкреНрд░рд╢реНрди
If `sin A = 9/41` compute cos ЁЭР┤ ЁЭСОЁЭСЫЁЭСС tan ЁЭР┤
рдЙрддреНрддрд░
`sin A = 9/41`
`sin A = "ЁЭСЬЁЭСЭЁЭСЭЁЭСЬЁЭСаЁЭСЦЁЭСбЁЭСТ ЁЭСаЁЭСЦЁЭССЁЭСТ"/"ЁЭСОЁЭССЁЭСЧЁЭСОЁЭСРЁЭСТЁЭСЫЁЭСб ЁЭСаЁЭСЦЁЭССЁЭСТ" = 9/41`
Consider the right-angled triangle ABC,
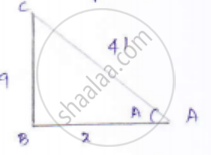
Let x be the adjacent side
By applying Pythagorean
ЁЭР┤ЁЭР╢2 = ЁЭР┤ЁЭР╡2 + ЁЭР╡ЁЭР╢2
412 = 122 + 92
ЁЭСе2 = 412 − 92
ЁЭСе = 40
`cos A = "ЁЭСОЁЭССЁЭСЧЁЭСОЁЭСРЁЭСТЁЭСЫЁЭСб ЁЭСаЁЭСЦЁЭССЁЭСТ"/"тДОЁЭСжЁЭСЭЁЭСЬЁЭСбЁЭСТЁЭСЫЁЭСвЁЭСаЁЭСТ" = 40/41`
`tan A = "ЁЭСЬЁЭСЭЁЭСЭЁЭСЬЁЭСаЁЭСЦЁЭСбЁЭСТ ЁЭСаЁЭСЦЁЭССЁЭСТ"/"ЁЭР╗ЁЭСжЁЭСЭЁЭСЬЁЭСбЁЭСТЁЭСЫЁЭСвЁЭСаЁЭСТ ЁЭСаЁЭСЦЁЭССЁЭСТ" = 9/40`
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНтАНрди
if `sin theta = 3/5 " evaluate " (cos theta - 1/(tan theta))/(2 cot theta)`
f θ = 30°, verify that cos 3θ = 4 cos3 θ − 3 cos θ
If sin θ = cos (θ – 45°), where θ – 45° are acute angles, find the degree measure of θ
If cos θ = `3/5` , show that `((sin theta - cot theta ))/(2tan theta)=3/160`
If sin ∝ = `1/2` prove that (3cos∝ - `4cos^2` ∝)=0
Evaluate:
`2cos^2 60^0+3 sin^2 45^0 - 3 sin^2 30^0 + 2 cos^2 90 ^0`
If A = 450, verify that :
(i) sin 2A = 2 sin A cos A
In the adjoining figure, ΔABC is a right-angled triangle in which ∠B = 900, ∠300 and AC = 20cm. Find (i) BC, (ii) AB.
sin20° = cos ______°
In ΔABC, ∠A = 90°. If AB = 5 units and AC = 12 units, find: sinB
