Advertisements
Advertisements
प्रश्न
If sin ∝ = `1/2` prove that (3cos∝ - `4cos^2` ∝)=0
उत्तर
𝐿𝐻𝑆 = (3𝑐𝑜𝑠𝑎 − `4 cos^3` 𝑎)
= 𝑐𝑜𝑠 𝑎(3 − `4 cos^2` 𝑎)
`= sqrt( 1 − sin^2 ∝) [3 − 4(1 − sin^2 ∝)]`
`= sqrt(1-(1/2)^2) [ 3-4 (1-(1/2)^2)]`
=`sqrt(1/1-1/4 [3-4 (1/1-1/4)])`
=`sqrt(3/4 [3-4(3/4)])`
=`sqrt(3/4 [3-3])`
=`sqrt(3/4[0])`
=0
=RHS.
APPEARS IN
संबंधित प्रश्न
In ΔPQR, right angled at Q, PQ = 4 cm and RQ = 3 cm. Find the values of sin P, sin R, sec P and sec R.
If cos θ = `3/5` , show that `((sin theta - cot theta ))/(2tan theta)=3/160`
If ∠A and ∠B are acute angles such that tan A= Tan B then prove that ∠A = ∠B
Show that:
(i)` (1-sin 60^0)/(cos 60^0)=(tan60^0-1)/(tan60^0+1)`
Show that:
(ii) `(cos30^0+sin 60^0)/(1+sin30^0+cos60^0)=cos 30^0`
From the following figure, find the values of:
- sin A
- cos A
- cot A
- sec C
- cosec C
- tan C

Form the following figure, find the values of:
- cos B
- tan C
- sin2B + cos2B
- sin B. cos C + cos B. sin C

In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
cotA = `(1)/(11)`
In the given figure, ΔABC is right angled at B.AD divides BC in the ratio 1 : 2. Find
(i) `("tan"∠"BAC")/("tan"∠"BAD")` (ii) `("cot"∠"BAC")/("cot"∠"BAD")`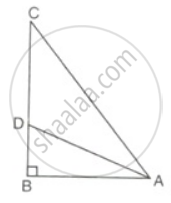
If sin θ = `"a"/sqrt("a"^2 + "b"^2)`, then show that b sin θ = a cos θ
