Advertisements
Advertisements
प्रश्न
From the following figure, find the values of:
- sin A
- cos A
- cot A
- sec C
- cosec C
- tan C

उत्तर
Given angle ABC = 90°
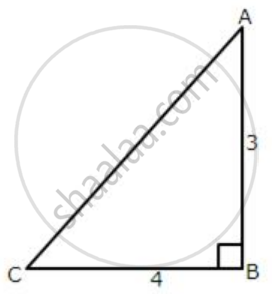
⇒ AC2 = AB2 + BC2 ...(AC is hypotenuse)
⇒ AC2 = 32 + 42
∴ AC2 = 9 + 16
∴ AC2 = 25
∴ AC2 = `sqrt25`
∴ AC = 5
(i) sin A = `" perpendicular"/" hypotenuse" = "BC"/ "AC" = 4/5`
(ii) cos A = `"base"/"hypotenuse" = "AB"/ "AC" = 3/5`
(iii) cot A = `"base "/"perpendicular" = "AB"/ "BC" = 3/4`
(iv) sec C = `"hypotenuse "/"base" = "AC"/ "BC" = 5/4`
(v) cosec C = `"hypotenuse"/" perpendicular" = "AC"/ "AB" = 5/3`
(vi) tan C = `" perpendicular"/"base" = "AB"/ "BC" = 3/4`
APPEARS IN
संबंधित प्रश्न
If `sin A = 9/41` compute cos 𝐴 𝑎𝑛𝑑 tan 𝐴
If θ = 30° verify `tan 2 theta = (2 tan theta)/(1 - tan^2 theta)`
If A = B = 60°, verify that cos (A − B) = cos A cos B + sin A sin B
If sin θ = cos (θ – 45°), where θ – 45° are acute angles, find the degree measure of θ
Evaluate:
`4/(cot^2 30^0) +1/(sin^2 30^0) -2 cos^2 45^0 - sin^2 0^0`
If A = 300 , verify that:
(i) sin 2A = `(2 tan A)/(1+tan^2A)`
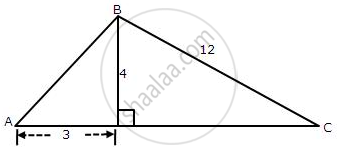
From the following figure, find the values of
(i) cos A
(ii) cosec A
(iii) tan2A - sec2A
(iv) sin C
(v) sec C
(vi) cot2 C - ` 1 / sin^2 "c"`
In the given figure, AD is the median on BC from A. If AD = 8 cm and BC = 12 cm, find the value of cos y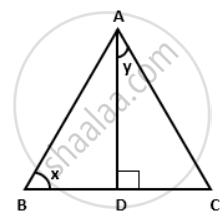
If 3 cot A = 2, then find the value of `(4sin"A" - 3cos"A")/(2sin"A" + 3cos"A")`
If A + B = 90°, cot B = `3/4` then tan A is equal to ______.
