Advertisements
Advertisements
प्रश्न
If A = B = 60°, verify that cos (A − B) = cos A cos B + sin A sin B
उत्तर
Given
A = B = 60°......(1)
To verify:
cos (A − B) = cos A cos B + sin A sin B
Now consider the left-hand side of the expression to be verified in equation (2)
Therefore,
cos (A − B) = cos (60 - 60)
= cos 0
= 1
Now consider the right-hand side of the expression to be verified in equation (2)
Therefore,
`cosAcosB + sin A sin B = cosBcosB + sin B sin B`
`= cos^2B + sin^2 B`
= 1
Hence it is verified that, cos (A − B) = cos A cos B + sin A sin B
APPEARS IN
संबंधित प्रश्न
If `sin (A – B) = 1/2` and `cos (A + B) = 1/2`, `0^@` < A + `B <= 90^@`, A > B Find A and B.
In right angled triangle ΔABC at B, ∠A = ∠C. Find the values of sin A sin B + cos A cos B
Show that:
(ii) `(cos30^0+sin 60^0)/(1+sin30^0+cos60^0)=cos 30^0`
If A = 600 and B = 300, verify that:
(i) sin (A – B) = sin A cos B – cos A sin B
Given: sec A = `( 29 )/(21), "evaluate : sin A" - 1/tan "A"`
Given: sin θ = `p/q`.
Find cos θ + sin θ in terms of p and q.
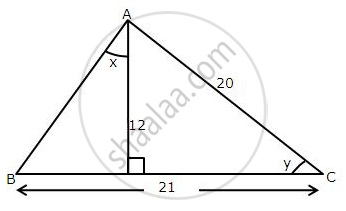
Use the information given in the following figure to evaluate:
`(10)/sin x + (6)/sin y – 6 cot y`.
In a right-angled triangle PQR, ∠PQR = 90°, QS ⊥ PR and tan R =`(5)/(12)`, find the value of sin ∠PQS
If sin A = `(7)/(25)`, find the value of : cot2A - cosec2A
If sin θ = `"a"/sqrt("a"^2 + "b"^2)`, then show that b sin θ = a cos θ
