Advertisements
Advertisements
प्रश्न
In ΔPQR, right angled at Q, PQ = 4 cm and RQ = 3 cm. Find the values of sin P, sin R, sec P and sec R.
उत्तर
ΔPQR right angled at Q.
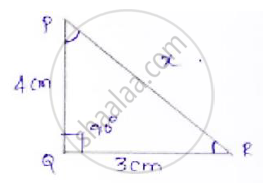
Let x be the hypotenuse
By applying Pythagoras
𝑃𝑅2 = 𝑃𝑄2 + 𝑄𝑅2
𝑥2 = 42 + 32
𝑥2 = 16 + 9
`∴ x = sqrt25 = 5`
Find sin 𝑃 , sin 𝑅, sec 𝑃, sec 𝑅
At LP, opposite side = 3 cm
Adjacent side = 4 cm
Hypotenuse = 5
`sin P = "𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑠𝑖𝑑𝑒"/"𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒" = 3/5`
`sec P = "𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒"/"𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 𝑠𝑖𝑑𝑒" = 5/4`
At LK, opposite side = 4 cm
Adjacent side = 3 cm
Hypotenuse = 5 cm
`sin R = 4/5`
`sec R = 5/3`
APPEARS IN
संबंधित प्रश्न
If sec 2A = cosec (A – 42°) where 2A is an acute angle. Find the value of A.
If sin θ ,` sqrt (3)/2` find the value of all T- ratios of θ .
In a ΔABC , ∠B = 90° , AB= 24 cm and BC = 7 cm find (i) sin A (ii) cos A (iii) sin C (iv) cos C
If ∠A and ∠B are acute angles such that tan A= Tan B then prove that ∠A = ∠B
Show that:
(ii) `(cos30^0+sin 60^0)/(1+sin30^0+cos60^0)=cos 30^0`
Verify each of the following:
(ii)`cos 60^0 cos 30^0+ sin 60^0 sin30^0`
Verify each of the following:
(iii) `2 sin 30^0 cos 30^0`
If A = 450, verify that :
(i) sin 2A = 2 sin A cos A
In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: 4sin2R - `(1)/("tan"^2"P")`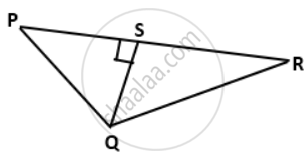
In the given figure, AD is the median on BC from A. If AD = 8 cm and BC = 12 cm, find the value of `(1)/("sin"^2 x) - (1)/("tan"^2 x)`
