Advertisements
Advertisements
प्रश्न
In the given figure, AD is the median on BC from A. If AD = 8 cm and BC = 12 cm, find the value of `(1)/("sin"^2 x) - (1)/("tan"^2 x)`
उत्तर
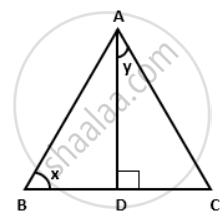
Since AD is median on BC, we have
BD = DC = `(1)/(2) xx "BC" = (1)/(2) xx 12` = 6cm
ΔADB is a right-angled triangle.
∴ AB2
= AD2 + BD2
= 82 + 62
= 64 + 36
= 100
⇒ AB = 10cm
ΔADC is a right-angled triangle.
∴ AC2
= AD2 + DC2
= 82 + 62
= 64 + 36
= 100
⇒ AC = 10cm
`(1)/("sin"^2 x) - (1)/("tan"^2 x)`
= `(1)/(4/5)^2 - (1)/(4/3)^2`
= `(25)/(16) - (9)/(16)`
= `(16)/(16)`
= 1.
APPEARS IN
संबंधित प्रश्न
If θ = 30° verify that `sin 2theta = (2 tan theta)/(1 + tan^2 theta)`
If sin A = `9/41` find all the values of cos A and tan A
If tan θ = `4/3`, show that `(sintheta + cos theta )=7/5`
Evaluate:
`(sin30°)/(cos 45°)+(cot45°)/(sec60° )- (sin60°)/(tan45°)+(cos30°)/(sin90°)`
Evaluate:
`(5 cos^2 60^circ + 4 sec^2 30^circ - tan^2 45^circ)/(sin^2 30^circ + cos^2 30^circ)`
Show that:
(ii) `(cos30^0+sin 60^0)/(1+sin30^0+cos60^0)=cos 30^0`
`(cos 28°)/(sin 62°)` = ?
From the following figure, find the values of:
- sin A
- cos A
- cot A
- sec C
- cosec C
- tan C

If sin A = `(7)/(25)`, find the value of : `(2"tanA")/"cot A - sin A"`
From the given figure, find the values of cos C
