Advertisements
Advertisements
प्रश्न
In the given figure, triangle ABC is right-angled at B. D is the foot of the perpendicular from B to AC. Given that BC = 3 cm and AB = 4 cm.
find :
- tan ∠DBC
- sin ∠DBA

उत्तर
Since the triangle ABC is a right-angled triangle, so using the Pythagorean Theorem,
AC2 = AB2 + BC2
AC2 = 42 + 32
AC2 = 16 + 9
AC2 = 25
AC = `sqrt25`
AC = 5
In ΔBCD
Cd2 + BD2 = BC2
y2 + x2 = (3)2
y2 + x2 = 9 (1)
In ΔABD
AD2 + BD2 = 16
(5 - y)2 + x2 = 16 ...(2)
subtracting (2) from (1) we get
(5 - y)2 - y2 = 7
25 + y2 - 10y - y2 = 7
18 =10y
1.8 = y
CD = 1.8
AD = 5 - 1.8
CD = 1.8, AD = 3.2, BD = 2.4
Now,
(1.8)2 + x2 = 9
x2 = 9 - 3.24
x2 = 5.76
x2 = 2.4
BD = 2.4
- tan ∠DBC = `(CD)/(BD) = 1.8/2.4 = 3/4`
- sin ∠DBA = `(AD)/(AB) = 3.2/4 = 4/5`
APPEARS IN
संबंधित प्रश्न
If `sin A = 9/41` compute cos 𝐴 𝑎𝑛𝑑 tan 𝐴
if `cos theta = 5/13` find the value of `(sin^2 theta - cos^2 theta)/(2 sin theta cos theta) = 3/5`
if `sin theta = 3/5 " evaluate " (cos theta - 1/(tan theta))/(2 cot theta)`
If sin 3θ = cos (θ – 6°) where 3θ and θ − 6° are acute angles, find the value of θ.
If sin A = `9/41` find all the values of cos A and tan A
If sin θ = `a/b`, show that `(sectheta + tan theta) = sqrt((b+a)/(b-a))`
In the given figure;
BC = 15 cm and sin B = `(4)/(5)`
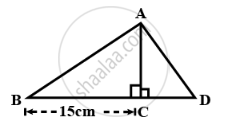
- Calculate the measure of AB and AC.
- Now, if tan ∠ADC = 1; calculate the measures of CD and AD.
Also, show that: tan2B - `1/cos^2 "B" = – 1 .`
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
cose C = `(15)/(11)`
In the given figure, AD is the median on BC from A. If AD = 8 cm and BC = 12 cm, find the value of tan x. cot y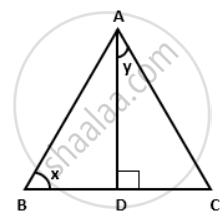
In a right-angled triangle PQR, ∠PQR = 90°, QS ⊥ PR and tan R =`(5)/(12)`, find the value of tan ∠SQR
