Advertisements
Advertisements
प्रश्न
In rectangle ABCD AB = 20cm ∠BAC = 60° BC, calculate side BC and diagonals AC and BD.
उत्तर
We have drawn the following figure
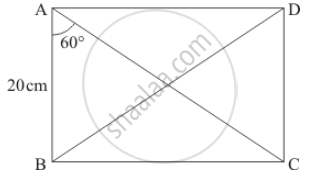
Since ABCD is a rectangle
Therefore
`∠ABC = ∠BCD = 90^@`
Now, consider ΔABC
We know that sum of all the angles of any triangle is 180º
Therefore,
∠BAC + ∠ABC + ∠ACB = 180° .....(1)
Now by substituting the values of known angles ∠BAC and ∠ABC inn equation (1)
We get
`60^@ + 90^@ + ∠ACB = 180^@`
`=> 150^@ + ∠ACb = 180^@`
`=> ∠ACB = 1806@ - 150^@`
`=> ∠ACb = 30^@`
Now in ΔABC
We know that
`cos A = cos 60^@`
`=> (AB)/(AC) = 60^@` ....(2)
Now we have,
`AB = 20 cm and cos 60^@ = 1/2`
Therefore by substituting above values in equation (2)
We get,
`cos A = cos 60^@`
`=> 20/(AC) = 1/2`
Now by cross multiplying we get,
`20 xx 2 = 1 xx AC`
=> 40 = AC
`=> AC = 40` ....(3)
Now in ΔABC
We know that,
`sin A = sin 60^@`
`=> (BC)/(AC) = sin 60^@` .....(4)
Now we have from equation (3),
`AC = 40 cm and sin 60^@ = sqrt3/2`
Therefore by substituting above values in equation (4)
We get,
`sin A = sin 60^@`
`=> (BC)/40 = sqrt3/2`
Now by cross multiplying we get,
`BC xx 2 = sqrt3 xx 40`
`=> BC = (sqrt3 xx 40)/2`
`=> BC = 20sqrt3`
Therefore
`BC = 20sqrt3 m` .....(5)
Since ABCD is a rectangle
Therefore,
AB = CD = 20 cm ....(6)
And
`BC = AD = 20sqrt3` cm .....(7)
Now in ΔBCD
We know that,
`tan B = (CD)/(BC)`
Now by substituting the values of sides from equation (6) and (7)
We get,
`tan B = 20/(20sqrt3)`
`=> tan B = 1/sqrt3`
Since
`tan 30^@ = 1/sqrt3`
Therefore ∠B = 30°
That is in ΔBCD
∠DBC = 30° ....(8)
Now in ΔBCD
We know that,
`cos B = (BC)/(BD)`
From equation (7)and (8)
`=> cos 30^@ = (20sqrt3)/(BD)`
Since
`cos 30^@ = sqrt3/2`
Therefore,
`sqrt3/2 = (20sqrt3)/(BD)`
Now by cross multiplying we get,
`sqrt3 xx (BD) = 20sqrt3 xx 2`
`=> sqrt3 xx BD = 40sqrt3`
`=> BD = (40sqrt3)/sqrt3`
=> BD = 4
Therfore
BC= 40 cm ...(9)
Hence from equation (3), (5) and (9)
`AC = 40 cm, BC = 20sqrt3 cm, BD = 40 cm`
APPEARS IN
संबंधित प्रश्न
If A = B = 60°, verify that sin (A − B) = sin A cos B − cos A sin B
If tan θ = `4/3`, show that `(sintheta + cos theta )=7/5`
If ∠A and ∠B are acute angles such that sin A = Sin B prove that ∠A = ∠B.
If A = 600 and B = 300, verify that:
(i) sin (A – B) = sin A cos B – cos A sin B
From the following figure, find the values of :
(i) sin A
(ii) sec A
(iii) cos2 A + sin2A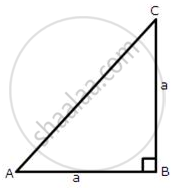
In the figure given below, ABC is an isosceles triangle with BC = 8 cm and AB = AC = 5 cm. Find:
(i) sin B
(ii) tan C
(iii) sin2 B + cos2B
(iv) tan C - cot B
Given : 5 cos A - 12 sin A = 0; evaluate:
`(sin "A"+cos"A")/(2 cos"A"– sin"A")`
In ΔABC, ∠B = 90°. If AB = 12units and BC = 5units, find: tan A
If cosB = `(1)/(3)` and ∠C = 90°, find sin A, and B and cot A.
If 3 cot A = 2, then find the value of `(4sin"A" - 3cos"A")/(2sin"A" + 3cos"A")`
