Advertisements
Advertisements
प्रश्न
In rectangle ABCD AB = 20cm ∠BAC = 60° BC, calculate side BC and diagonals AC and BD.
उत्तर
We have drawn the following figure
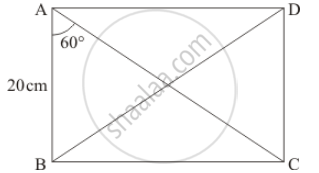
Since ABCD is a rectangle
Therefore
`∠ABC = ∠BCD = 90^@`
Now, consider ΔABC
We know that sum of all the angles of any triangle is 180º
Therefore,
∠BAC + ∠ABC + ∠ACB = 180° .....(1)
Now by substituting the values of known angles ∠BAC and ∠ABC inn equation (1)
We get
`60^@ + 90^@ + ∠ACB = 180^@`
`=> 150^@ + ∠ACb = 180^@`
`=> ∠ACB = 1806@ - 150^@`
`=> ∠ACb = 30^@`
Now in ΔABC
We know that
`cos A = cos 60^@`
`=> (AB)/(AC) = 60^@` ....(2)
Now we have,
`AB = 20 cm and cos 60^@ = 1/2`
Therefore by substituting above values in equation (2)
We get,
`cos A = cos 60^@`
`=> 20/(AC) = 1/2`
Now by cross multiplying we get,
`20 xx 2 = 1 xx AC`
=> 40 = AC
`=> AC = 40` ....(3)
Now in ΔABC
We know that,
`sin A = sin 60^@`
`=> (BC)/(AC) = sin 60^@` .....(4)
Now we have from equation (3),
`AC = 40 cm and sin 60^@ = sqrt3/2`
Therefore by substituting above values in equation (4)
We get,
`sin A = sin 60^@`
`=> (BC)/40 = sqrt3/2`
Now by cross multiplying we get,
`BC xx 2 = sqrt3 xx 40`
`=> BC = (sqrt3 xx 40)/2`
`=> BC = 20sqrt3`
Therefore
`BC = 20sqrt3 m` .....(5)
Since ABCD is a rectangle
Therefore,
AB = CD = 20 cm ....(6)
And
`BC = AD = 20sqrt3` cm .....(7)
Now in ΔBCD
We know that,
`tan B = (CD)/(BC)`
Now by substituting the values of sides from equation (6) and (7)
We get,
`tan B = 20/(20sqrt3)`
`=> tan B = 1/sqrt3`
Since
`tan 30^@ = 1/sqrt3`
Therefore ∠B = 30°
That is in ΔBCD
∠DBC = 30° ....(8)
Now in ΔBCD
We know that,
`cos B = (BC)/(BD)`
From equation (7)and (8)
`=> cos 30^@ = (20sqrt3)/(BD)`
Since
`cos 30^@ = sqrt3/2`
Therefore,
`sqrt3/2 = (20sqrt3)/(BD)`
Now by cross multiplying we get,
`sqrt3 xx (BD) = 20sqrt3 xx 2`
`=> sqrt3 xx BD = 40sqrt3`
`=> BD = (40sqrt3)/sqrt3`
=> BD = 4
Therfore
BC= 40 cm ...(9)
Hence from equation (3), (5) and (9)
`AC = 40 cm, BC = 20sqrt3 cm, BD = 40 cm`
APPEARS IN
संबंधित प्रश्न
if `sec theta = 5/4` find the value of `(sin theta - 2 cos theta)/(tan theta - cot theta)`
If 8 tan A = 15, find sin A – cos A.
In a ΔABC, right angled at A, if tan C = `sqrt3` , find the value of sin B cos C + cos B sin C.
If θ = 30° verify that `sin 2theta = (2 tan theta)/(1 + tan^2 theta)`
If sin 3θ = cos (θ – 6°) where 3θ and θ − 6° are acute angles, find the value of θ.
If sin θ = `a/b`, show that `(sectheta + tan theta) = sqrt((b+a)/(b-a))`
If cos θ = `3/5` , show that `((sin theta - cot theta ))/(2tan theta)=3/160`
If sin (A+B) = sin A cos B + cos A sin B and cos (A-B) = cos A cos B + sin A sin B
(i) sin (750)
(ii) cos (150)
Given: cos A = 0.6; find all other trigonometrical ratios for angle A.
In the given figure, ΔABC is right angled at B.AD divides BC in the ratio 1 : 2. Find
(i) `("tan"∠"BAC")/("tan"∠"BAD")` (ii) `("cot"∠"BAC")/("cot"∠"BAD")`