Advertisements
Advertisements
प्रश्न
If 8 tan A = 15, find sin A – cos A.
उत्तर
8 tan A = 15 find. Sin A – cos A
`tan A = 15/8`
tan A = `"Opposite side"/"adjacent side"`
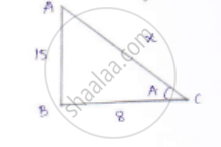
Let x be the hypotenuse By applying theorem
𝐴𝐶2 = 𝐴𝐵2 + 𝐵𝐶2
𝑥2 = 152 + 82
𝑥2 = 225 + 64
𝑥2 = 289 ⇒ x = 17
`sin A = (AB)/(AC) = 15/17`
`sin A - cos A = 15/17 - 8/17`
`= 7/17`
APPEARS IN
संबंधित प्रश्न
If `sin A = 9/41` compute cos 𝐴 𝑎𝑛𝑑 tan 𝐴
In ∆PQR, right-angled at Q, PQ = 3 cm and PR = 6 cm. Determine ∠P and ∠R.
If sec `theta = 17/8 ` verify that `((3-4sin^2theta)/(4 cos^2theta -3))=((3-tan^2theta)/(1-tan^2theta))`
If x = cosec A +cos A and y = cosec A – cos A then prove that `(2/(x+y))^2 + ((x-y)/2)^2` = 1
Show that:
(i)` (1-sin 60^0)/(cos 60^0)=(tan60^0-1)/(tan60^0+1)`
In the adjoining figure, ΔABC is a right-angled triangle in which ∠B = 900, ∠300 and AC = 20cm. Find (i) BC, (ii) AB.
If 5 cot θ = 12, find the value of : Cosec θ+ sec θ
In triangle ABC; ∠ABC = 90°, ∠CAB = x°, tan x° = `(3)/(4)` and BC = 15 cm. Find the measures of AB and AC.
In rhombus ABCD, diagonals AC and BD intersect each other at point O.
If cosine of angle CAB is 0.6 and OB = 8 cm, find the lengths of the side and the diagonals of the rhombus.
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
cose C = `(15)/(11)`
