Advertisements
Advertisements
प्रश्न
In rhombus ABCD, diagonals AC and BD intersect each other at point O.
If cosine of angle CAB is 0.6 and OB = 8 cm, find the lengths of the side and the diagonals of the rhombus.
उत्तर
Consider the figure :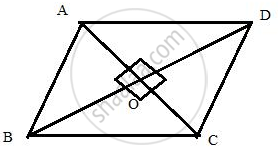
The diagonals of a rhombus bisect each other perpendicularly
cos ∠CAB = `(6)/(10) = (3)/(5)`
i.e.`"base"/"hypotenuse" = "OA"/"AB" = (3)/(5)`
Therefore if length of base = 3x, length of hypotenuse = 5x
Since
OB2 + OA2 = AB2 ...[ Using Pythagoras Theorem ]
(5x)2 – (3x)2 = OB2
OB2 = 16x2
∴ OB = 4x
Now
OB = 8
4x = 8
x = 2
Therefore
AB = 5x
= 5 x 2
= 10 cm
And
OA = 3x
= 3 x 2
= 6 cm
Since the sides of a rhombus are equal so the length of the side of the rhombus
The diagonals are
BD = 8 x 2
= 16 cm
AC = 6 x 2
= 12 cm
APPEARS IN
संबंधित प्रश्न
If 3tan θ 4 , show that `((4cos theta - sin theta ))/((4 cos theta + sin theta))=4/5`
If 3 cot θ 4 , show that`((1-tan^2theta))/((1+tan^2theta)) = (cos^2theta - sin^2theta)`
If x = cot A + cos A and y = cot A – cos A then prove that `((x-y)/(x+y))^2 + ((x-y)/2)^2=1`
Verify each of the following:
(iv) `2 sin 45^0 cos 45^0`
If A = 600 and B = 300, verify that:
(i) sin (A + B) = sin A cos B + cos A sin B
Using the formula, cos A = `sqrt((1+cos2A)/2) ,`find the value of cos 300, it being given that cos 600 = `1/2`.
In the adjoining figure, ΔABC is a right-angled triangle in which ∠B = 900, ∠300 and AC = 20cm. Find (i) BC, (ii) AB.
If sin A = `(sqrt3)/(2)` and cos B = `(sqrt3)/(2)` , find the value of : `(tan"A" – tan"B")/(1+tan"A" tan"B")`
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
cosB = `(4)/(5)`
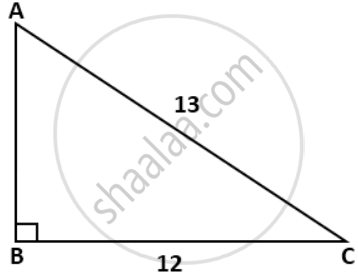
In the given figure, AC = 13cm, BC = 12 cm and ∠B = 90°. Without using tables, find the values of: `("cos A" - "sin A")/("cos A" + "sin A")`