Advertisements
Advertisements
प्रश्न
In rhombus ABCD, diagonals AC and BD intersect each other at point O.
If cosine of angle CAB is 0.6 and OB = 8 cm, find the lengths of the side and the diagonals of the rhombus.
उत्तर
Consider the figure :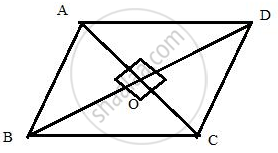
The diagonals of a rhombus bisect each other perpendicularly
cos ∠CAB = `(6)/(10) = (3)/(5)`
i.e.`"base"/"hypotenuse" = "OA"/"AB" = (3)/(5)`
Therefore if length of base = 3x, length of hypotenuse = 5x
Since
OB2 + OA2 = AB2 ...[ Using Pythagoras Theorem ]
(5x)2 – (3x)2 = OB2
OB2 = 16x2
∴ OB = 4x
Now
OB = 8
4x = 8
x = 2
Therefore
AB = 5x
= 5 x 2
= 10 cm
And
OA = 3x
= 3 x 2
= 6 cm
Since the sides of a rhombus are equal so the length of the side of the rhombus
The diagonals are
BD = 8 x 2
= 16 cm
AC = 6 x 2
= 12 cm
APPEARS IN
संबंधित प्रश्न
If a right ΔABC , right-angled at B, if tan A=1 then verify that 2sin A . cos A = 1
Evaluate:
`(sin30°)/(cos 45°)+(cot45°)/(sec60° )- (sin60°)/(tan45°)+(cos30°)/(sin90°)`
If A = 600 and B = 300, verify that:
(i) sin (A + B) = sin A cos B + cos A sin B
If A = 600 and B = 300, verify that:
cos (A + B) = cos A cos B - sin A sin B
If sec A = `sqrt2` , find : `(3cot^2 "A"+ 2 sin^2 "A")/ (tan^2 "A" – cos ^2 "A")`.
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
sinA = `(12)/(13)`
In ΔABC, ∠A = 90°. If AB = 5 units and AC = 12 units, find: cos C
In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: sin P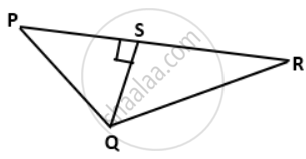
In the given figure, AD is the median on BC from A. If AD = 8 cm and BC = 12 cm, find the value of tan x. cot y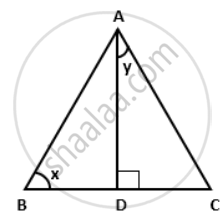
If cos θ : sin θ = 1 : 2, then find the value of `(8costheta - 2sintheta)/(4costheta + 2sintheta`
