Advertisements
Advertisements
प्रश्न
In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: sin P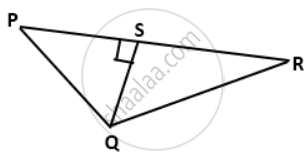
उत्तर
ΔQSP is a right-angled triangle.
∴ PQ2 = QS2 + PS2
= 32 + 42
= 9 + 16
= 25
⇒ PQ = 5cm
sin P
= `"QS"/"PQ"`
= `(3)/(5)`.
APPEARS IN
संबंधित प्रश्न
If A = B = 60°. Verify `tan (A - B) = (tan A - tan B)/(1 + tan tan B)`
In rectangle ABCD AB = 20cm ∠BAC = 60° BC, calculate side BC and diagonals AC and BD.
If tan θ = `4/3`, show that `(sintheta + cos theta )=7/5`
If tan `theta = a/b`, show that `((a sin theta - b cos theta))/((a sin theta + bcos theta))= ((a^2-b^2))/(a^2+b^2)`
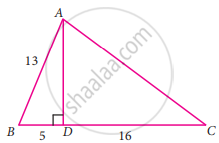
From the following figure, find the values of
(i) cos A
(ii) cosec A
(iii) tan2A - sec2A
(iv) sin C
(v) sec C
(vi) cot2 C - ` 1 / sin^2 "c"`
Given : sin A = `(3)/(5)` , find : (i) tan A (ii) cos A
If 5 cot θ = 12, find the value of : Cosec θ+ sec θ
In triangle ABC, ∠B = 90° and tan A = 0.75. If AC = 30 cm, find the lengths of AB and BC.
If cosB = `(1)/(3)` and ∠C = 90°, find sin A, and B and cot A.
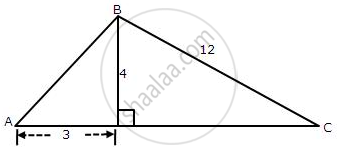
From the given figure, find the values of tan C