Advertisements
Advertisements
प्रश्न
If 8 tanθ = 15, find (i) sinθ, (ii) cotθ, (iii) sin2θ - cot2θ
उत्तर
8tan θ = 15
⇒ tan θ = `(15)/(8) = "Perpendicular"/"Base"`
Hypotenuse
= `sqrt(("Perpendicular")^2 + ("Base")^2`
= `sqrt(15^2 + 8^2)`
= `sqrt(225 + 64)`
= `sqrt(289)`
= 17
(i) sin θ = `"Perpendicular"/"Hypotenuse" = (15)/(17)`
cot θ = `(1)/"tan θ " = (8)/(15)`
(iii) sin2θ - cot2θ
= (sin θ + cot θ)(sin θ - cot θ)
= `(15/17 + 8/15)(15/17 - 8/15)`
= `((225 + 136)/225)((225 - 136)/225)`
= `(361/225)(89/255)`
= `(32129)/(65025)`.
APPEARS IN
संबंधित प्रश्न
If 3 cot A = 4, Check whether `((1-tan^2 A)/(1+tan^2 A)) = cos^2 "A" - sin^2 "A"` or not.
In ∆PQR, right-angled at Q, PQ = 3 cm and PR = 6 cm. Determine ∠P and ∠R.
If cosec θ = `sqrt(10)` find all the values of all T-ratios of θ
If 3 cot θ 4 , show that`((1-tan^2theta))/((1+tan^2theta)) = (cos^2theta - sin^2theta)`
Evaluate:
cos450 cos300 + sin450 sin300
If A = 450, verify that :
(i) sin 2A = 2 sin A cos A
In the following figure:
AD ⊥ BC, AC = 26 CD = 10, BC = 42, ∠DAC = x and ∠B = y.
Find the value of :
(i) cot x
(ii) `1/sin^2 y – 1/tan^2 y`
(iii) `6/cos x – 5/cos y + 8 tan y`.
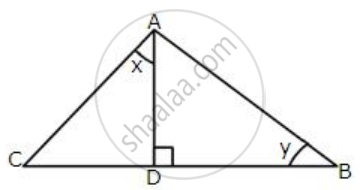
From the following figure, find:
(i) y
(ii) sin x°
(iii) (sec x° - tan x°) (sec x° + tan x°)

In triangle ABC, AB = AC = 15 cm and BC = 18 cm. Find:
- cos B
- sin C
- tan2 B - sec2 B + 2
Assertion (A): For 0 < 0 ≤ 90°, cosec θ – cot θ and cosec θ + cot θ are reciprocal of each other.
Reason (R): cot2 θ – cosec2 θ = 1.
