Advertisements
Advertisements
प्रश्न
If 3tan θ 4 , show that `((4cos theta - sin theta ))/((4 cos theta + sin theta))=4/5`
उत्तर
Let us consider a right ΔABC right angled at B and ∠𝐶 = 𝜃.
We know that tan 𝜃 =`(AB)/(BC) = 4/3`
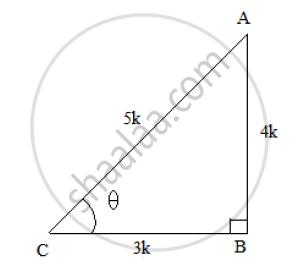
So, if BC = 3k, then AB = 4k, where k is a positive number.
Using Pythagoras theorem, we have:
`AC^2 = AB^2 + BC^2`
`⟹ AC^2 = 16K^2 + 9K^2`
`⟹ AC^2 = 25K^2`
⟹ AC = 5k
Now, we have:
`sin theta = (AB)/(AC) = (4K)/(5K)=4/5`
`Cos theta = (BC)/(AC) = (3K)/(5K)=3/5`
Substituting these values in the given expression, we get:
`(4 cos theta - sin theta)/(2 cos theta + sin theta)`
`= (4(3/5)-4/5)/(2 (3/5)+4/5)`
`= (12/5-4/5)/(6/5+4/5)`
`= ((12-4)/5)/((6+4)/5)`
`= 8/10 = 4/5 = RHS`
i.e., LHS = RHS
Hence proved.
APPEARS IN
संबंधित प्रश्न
If ∠A and ∠P are acute angles such that tan A = tan P, then show that ∠A = ∠P.
sin20° = cos ______°
From the following figure, find the values of
(i) sin B
(ii) tan C
(iii) sec2 B - tan2B
(iv) sin2C + cos2C
Given: sec A = `( 29 )/(21), "evaluate : sin A" - 1/tan "A"`
In rhombus ABCD, diagonals AC and BD intersect each other at point O.
If cosine of angle CAB is 0.6 and OB = 8 cm, find the lengths of the side and the diagonals of the rhombus.
In triangle ABC, AB = AC = 15 cm and BC = 18 cm. Find:
- cos B
- sin C
- tan2 B - sec2 B + 2
In ΔABC, ∠B = 90°. If AB = 12units and BC = 5units, find: tan A
In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: sin P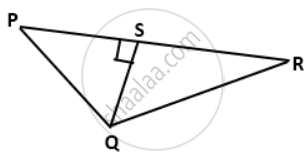
If sin A = `(7)/(25)`, find the value of : cot2A - cosec2A
Assertion (A): For 0 < 0 ≤ 90°, cosec θ – cot θ and cosec θ + cot θ are reciprocal of each other.
Reason (R): cot2 θ – cosec2 θ = 1.
