Advertisements
Advertisements
Question
If 3tan θ 4 , show that `((4cos theta - sin theta ))/((4 cos theta + sin theta))=4/5`
Solution
Let us consider a right ΔABC right angled at B and ∠𝐶 = 𝜃.
We know that tan 𝜃 =`(AB)/(BC) = 4/3`
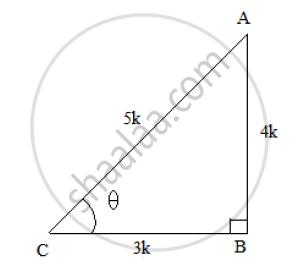
So, if BC = 3k, then AB = 4k, where k is a positive number.
Using Pythagoras theorem, we have:
`AC^2 = AB^2 + BC^2`
`⟹ AC^2 = 16K^2 + 9K^2`
`⟹ AC^2 = 25K^2`
⟹ AC = 5k
Now, we have:
`sin theta = (AB)/(AC) = (4K)/(5K)=4/5`
`Cos theta = (BC)/(AC) = (3K)/(5K)=3/5`
Substituting these values in the given expression, we get:
`(4 cos theta - sin theta)/(2 cos theta + sin theta)`
`= (4(3/5)-4/5)/(2 (3/5)+4/5)`
`= (12/5-4/5)/(6/5+4/5)`
`= ((12-4)/5)/((6+4)/5)`
`= 8/10 = 4/5 = RHS`
i.e., LHS = RHS
Hence proved.
APPEARS IN
RELATED QUESTIONS
From the following figure, find:
(i) y
(ii) sin x°
(iii) (sec x° - tan x°) (sec x° + tan x°)

In triangle ABC, AB = AC = 15 cm and BC = 18 cm, find cos ∠ABC.
If 3 cos A = 4 sin A, find the value of :
(i) cos A(ii) 3 - cot2 A + cosec2A.
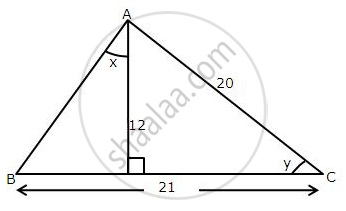
Use the information given in the following figure to evaluate:
`(10)/sin x + (6)/sin y – 6 cot y`.
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
sinB = `sqrt(3)/(2)`
If sin θ = `(8)/(17)`, find the other five trigonometric ratios.
If cos A = `3/5`, then find the value of `(sin"A" - cos"A")/(2tan"A")`
If cos A = `(2x)/(1 + x^2)`, then find the values of sin A and tan A in terms of x
From the given figure, prove that θ + ∅ = 90°. Also prove that there are two other right angled triangles. Find sin α, cos β and tan ∅
If A + B = 90°, cot B = `3/4` then tan A is equal to ______.
