Advertisements
Advertisements
Question
If 3 cot `theta = 2, `show that `((4 sin theta - 4 cos theta))/((2 sin theta + 6 cos theta ))=1/3`
Solution
It is given that cos 𝜃 = `2/3`
LHS = `( 4 sin theta -3 cos theta)/(2 sin theta + 6 cos theta)`
Dividing the above expression by sin 𝜃, 𝑤𝑒 𝑔𝑒𝑡:
`(4-3 cot theta)/(2+6 cot theta) [∵ cot theta = (cos theta)/(sin theta)]`
Now, substituting the values of cot 𝜃 𝑖𝑛 𝑡ℎ𝑒 𝑎𝑏𝑜𝑣𝑒 𝑒𝑥𝑝𝑟𝑒𝑠𝑠𝑖𝑜𝑛, 𝑤𝑒 𝑔𝑒𝑡:
`(4-3(2/3))/(2+6(2/3))`
=`(4-2)/(2+4)=2/6=1/3`
i.e., LHS = RHS
Hence proved.
APPEARS IN
RELATED QUESTIONS
If sin 3θ = cos (θ – 6°) where 3θ and θ − 6° are acute angles, find the value of θ.
If Sec 4A = cosec (A – 20°) where 4A is an acute angle, find the value of A.
If 3 cot θ 4 , show that`((1-tan^2theta))/((1+tan^2theta)) = (cos^2theta - sin^2theta)`
If A = 600 and B = 300, verify that:
(i) sin (A + B) = sin A cos B + cos A sin B
Given: sec A = `( 29 )/(21), "evaluate : sin A" - 1/tan "A"`
If 2 sin x = `sqrt3` , evaluate.
(i) 4 sin3 x - 3 sin x.
(ii) 3 cos x - 4 cos3 x.
If cosec A + sin A = 5`(1)/(5)`, find the value of cosec2A + sin2A.
In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: cot2P - cosec2P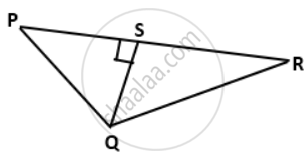
From the given figure, find the values of sin B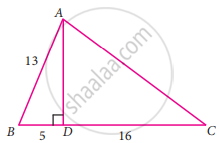
Statement A (Assertion): For 0 < θ ≤ 90°, cosec θ – cot θ and cosec θ + cot θ are reciprocal of each other.
Statement R (Reason): cosec2 θ – cot2 θ = 1
