Advertisements
Advertisements
प्रश्न
In a ΔABC, right angled at A, if tan C = `sqrt3` , find the value of sin B cos C + cos B sin C.
उत्तर
In a Δle ABC right angled at A tan C = `sqrt3`
Find sin B cos C + cos B sin C
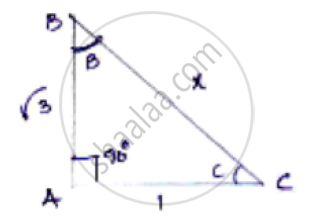
`tan c = sqrt3`
`tan c = "oppoite side"/"adjacent side"`
Let x be the hypotenuse By applying Pythagoras we get
`BC^2 = BA^2 + AC^2`
`x^2 = (sqrt3)^2 + 1^2`
x2 = Δ ⇒ x = 2
At ∠B, `sin B = (AC)/(BC) = 1/2`
`cos B = sqrt3/2`
At ∠C, `sin = sqrt3/2`
`cos c = 1/2`
On substitution we get
`=> 1/2 xx 1/2 + sqrt3/2 xx sqrt3/2`
`=> 1/4 + (sqrt3)/4 xx (sqrt3) = (sqrt3 xx sqrt3 + 1)/4 = (3 + 1)/4 = 4/4 = 1`
APPEARS IN
संबंधित प्रश्न
if `sec A = 5/4` verify that `(3 sin A - 4 sin^3 A)/(4 cos^3 A - 3 cos A) = (3 tan A - tan^3 A)/(1- 3 tan^2 A)`
If ∠A and ∠P are acute angles such that tan A = tan P, then show that ∠A = ∠P.
If sec θ = `5/4 ` show that `((sin θ - 2 cos θ))/(( tan θ - cot θ)) = 12/7`
If sin θ = `a/b`, show that `(sectheta + tan theta) = sqrt((b+a)/(b-a))`
Verify each of the following:
(ii)`cos 60^0 cos 30^0+ sin 60^0 sin30^0`
Verify each of the following:
(iv) `2 sin 45^0 cos 45^0`
If A = 450 , verify that:
(ii) cos 2A = 2 cos2 A – 1 = 1 – 2 sin2 A
If A = 600 and B = 300, verify that:
cos (A + B) = cos A cos B - sin A sin B
In the adjoining figure, ΔABC is right-angled at B and ∠A = 300. If BC = 6cm, find (i) AB, (ii) AC.
`(cos 28°)/(sin 62°)` = ?
