Advertisements
Advertisements
प्रश्न
In the adjoining figure, ΔABC is right-angled at B and ∠A = 300. If BC = 6cm, find (i) AB, (ii) AC.
उत्तर
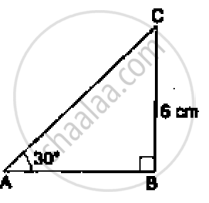
From the given right-angled triangle, we have:
`(BC)/(AB)= tan 30^0`
⇒`6/(AB) = 1/sqrt(3)`
⇒ `AB = 6 sqrt(3) cm`
Also, `(BC)/(AC) = sin 30^0`
⇒`6/(AC)=1/2`
⇒ `AC = (2xx6)=12 cm `
∴ AB = 6`sqrt(3)` cm and AC = 12 cm
APPEARS IN
संबंधित प्रश्न
If A = 30° B = 60° verify Sin (A + B) = Sin A Cos B + cos A sin B
If tan θ = `1/sqrt(7) `show that ` (cosec ^2 θ - sec^2 θ)/(cosec^2 θ + sec^2 θ ) = 3/4`
If sin ∝ = `1/2` prove that (3cos∝ - `4cos^2` ∝)=0
If a right ΔABC , right-angled at B, if tan A=1 then verify that 2sin A . cos A = 1
If x = cot A + cos A and y = cot A – cos A then prove that `((x-y)/(x+y))^2 + ((x-y)/2)^2=1`
If A and B are acute angles such that tan A =`1/3, tan B = 1/2 and tan (A + B) =` show that `A+B = 45^0`
If sin (A+B) = sin A cos B + cos A sin B and cos (A-B) = cos A cos B + sin A sin B
(i) sin (750)
(ii) cos (150)
In the given figure, AD is the median on BC from A. If AD = 8 cm and BC = 12 cm, find the value of cos y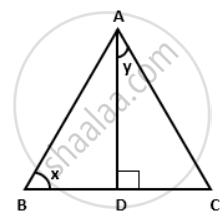
In a right-angled triangle PQR, ∠PQR = 90°, QS ⊥ PR and tan R =`(5)/(12)`, find the value of tan ∠SQR
From the given figure, find the values of cot B