Advertisements
Advertisements
प्रश्न
If tan θ = `1/sqrt(7) `show that ` (cosec ^2 θ - sec^2 θ)/(cosec^2 θ + sec^2 θ ) = 3/4`
उत्तर
Let us consider a right ΔABC, right angled at B and ∠𝐶 = 𝜃.
Now it is given that tan 𝜃 = `(AB)/(BC) = 1/(sqrt(7))`
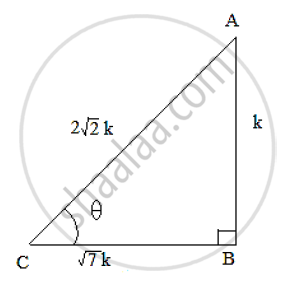
So, if AB = k, then BC = `sqrt(7) `𝑘, 𝑤ℎ𝑒𝑟 𝑘 𝑖𝑠 𝑎 𝑝𝑜𝑠𝑖𝑡𝑖𝑣𝑒 𝑛𝑢𝑚𝑏𝑒𝑟.
Using Pythagoras theorem, we have:
`AC^2 = AB^2 + BC^2`
`⟹ AC^2 = (k)^2 + (sqrt(7K)`
`⟹ AC^2 = K^2 + 7K^2`
`⟹ AC = 2sqrt(2K)`
Now, finding out the values of the other trigonometric ratios, we have:
sin θ = `(AB)/(AC) = K/(2sqrt(2k)) = 1/(2sqrt(2))`
cos θ = `( BC)/(AC) = (sqrt(7k))/(2 sqrt(2k)) = (sqrt(7))/(2sqrt(2))`
∴ 𝑐𝑜𝑠𝑒𝑐 𝜃 =`1/(sin θ) = 2 sqrt(2) and sec θ = 1/cos θ = (2sqrt(2))/(sqrt(7))`
Substituting the values of cosec θ and sec θ in the give expression, we get:
`(cosec^2 θ - sec^2 θ)/(cosec^2 θ + sec2 θ)`
=`(2 sqrt(2)^2-((2sqrt(2))/sqrt(7))^2)/(2sqrt({2)^2)+((2sqrt(2))/sqrt(7))^2)`
=`(8-(8/7))/(8+(8/7))`
= `((56-8)/7)/((56+8)/7)`
=`48/64 = 3/4 `= 𝑅𝐻𝑆
i.e., LHS = RHS
Hence proved.
APPEARS IN
संबंधित प्रश्न
If A = B = 60°, verify that sin (A − B) = sin A cos B − cos A sin B
In the figure of ΔPQR , ∠P = θ° and ∠R =∅° find
(i) `sqrt(X +1) cot ∅`
(ii)`sqrt( x^3 + x ^2) tantheta`
(iii) cos θ

Verify each of the following:
(iii) `2 sin 30^0 cos 30^0`
If A = 450, verify that :
(i) sin 2A = 2 sin A cos A
In the given figure, triangle ABC is right-angled at B. D is the foot of the perpendicular from B to AC. Given that BC = 3 cm and AB = 4 cm.
find :
- tan ∠DBC
- sin ∠DBA

In rectangle ABCD, diagonal BD = 26 cm and cotangent of angle ABD = 1.5. Find the area and the perimeter of the rectangle ABCD.
In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: 4sin2R - `(1)/("tan"^2"P")`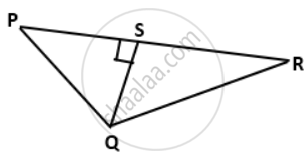
If sin A = `(7)/(25)`, find the value of : cot2A - cosec2A
In the given figure, AC = 13cm, BC = 12 cm and ∠B = 90°. Without using tables, find the values of: sin A cos A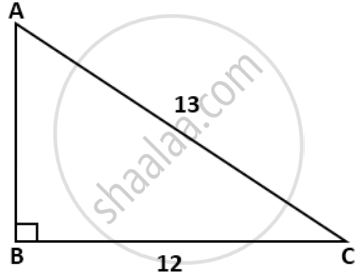
Evaluate: `5/(cot^2 30^circ) + 1/(sin^2 60^circ) - cot^2 45^circ + 2 sin^2 90^circ`.
