Advertisements
Advertisements
प्रश्न
In rectangle ABCD, diagonal BD = 26 cm and cotangent of angle ABD = 1.5. Find the area and the perimeter of the rectangle ABCD.
उत्तर
Consider the diagram:
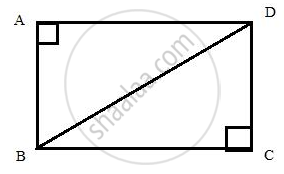
cot ∠ABD = `(15)/(10) = (3)/(2)`
i.e.`"base"/"perpendicular" = "AB"/"BD" = (3)/(2)`
Therefore, if length of base = 3x, length of perpendicular = 2x
Since
AB2 + AD2 = BD2 ...[Using Pythagoras Theorem]
(3x)2 + (2x)2 = BD2
BD2 = 13x2
∴ BD = `sqrt13x`
Now
BD = 26
`sqrt13x` = 26
x = `(26)/sqrt13`
Therefore
AD = 2x
= 2x `(26)/sqrt13`
= `(52)/sqrt13` cm
AB = 3x
= `3 xx (26)/sqrt13`
=`(78)/sqrt13` cm
Now
Area of rectangle ABCD = AB × AD
= `(78)/sqrt13 x (52)/sqrt13`
= 312 cm2
Perim of rectangle ABCD = 2 (AB + AD)
= 2 `((78)/sqrt13 + (52)/sqrt13)`
= `(260)/sqrt13`
= 20`sqrt13` cm
APPEARS IN
संबंधित प्रश्न
If 8 tan A = 15, find sin A – cos A.
If tan θ = `1/sqrt(7) `show that ` (cosec ^2 θ - sec^2 θ)/(cosec^2 θ + sec^2 θ ) = 3/4`
If 3tan θ 4 , show that `((4cos theta - sin theta ))/((4 cos theta + sin theta))=4/5`
If 3 cot θ 4 , show that`((1-tan^2theta))/((1+tan^2theta)) = (cos^2theta - sin^2theta)`
If cot θ= 1; find the value of: 5 tan2 θ+ 2 sin2 θ- 3
In the given figure;
BC = 15 cm and sin B = `(4)/(5)`
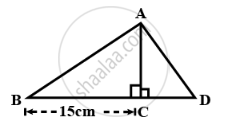
- Calculate the measure of AB and AC.
- Now, if tan ∠ADC = 1; calculate the measures of CD and AD.
Also, show that: tan2B - `1/cos^2 "B" = – 1 .`
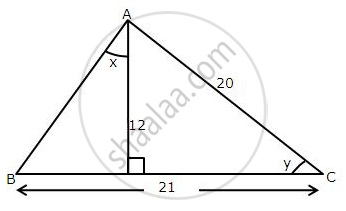
Use the information given in the following figure to evaluate:
`(10)/sin x + (6)/sin y – 6 cot y`.
In an isosceles triangle ABC, AB = BC = 6 cm and ∠B = 90°. Find the values of cosec C
In the given figure, AD is the median on BC from A. If AD = 8 cm and BC = 12 cm, find the value of `(1)/("sin"^2 x) - (1)/("tan"^2 x)`
If sin A = `(7)/(25)`, find the value of : `"cos A" + (1)/"cot A"`
