Advertisements
Advertisements
प्रश्न
If sin A = cos A, find the value of 2 tan2A - 2 sec2 A + 5.
उत्तर
Consider the figure : 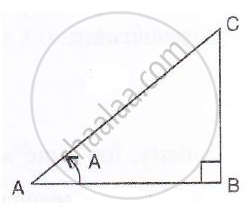
sin A = cos A
tan A = `(1)/(1)`
i.e.`"perpendicular"/"base" = "BC"/"AB" = (1)/(1)`
Therefore if length of perpendicular = x, length of base = x
Since
AB2 + BC2 = AC2 ...[ Using Pythagoras Theorem]
(x)2 + (x)2 = AC2
AC2 = 2x2
∴ AC = `sqrt2x`
Now
sec A = `"AC"/"AB" = sqrt2`
Therefore
2 tan2 A – 2sec2 A + 5
= 2(1)2 –2 (`sqrt2`)2 + 5
= 2 – 4 + 5
= 3
APPEARS IN
संबंधित प्रश्न
f θ = 30°, verify that cos 3θ = 4 cos3 θ − 3 cos θ
If A = B = 60°, verify that cos (A − B) = cos A cos B + sin A sin B
If sin A = `9/41` find all the values of cos A and tan A
If cot θ = `3/4` , show that `sqrt("sec θ - cosecθ"/"secθ + cosecθ" ) = 1/ sqrt(7)`
If sin ∝ = `1/2` prove that (3cos∝ - `4cos^2` ∝)=0
If a right ΔABC , right-angled at B, if tan A=1 then verify that 2sin A . cos A = 1
If A = 600 and B = 300, verify that:
(i) sin (A – B) = sin A cos B – cos A sin B
If 5 cot θ = 12, find the value of : Cosec θ+ sec θ
If cos A = `(2x)/(1 + x^2)`, then find the values of sin A and tan A in terms of x
Given that sin α = `1/2` and cos β = `1/2`, then the value of α + β is ______.
