Advertisements
Advertisements
प्रश्न
cos 40° = sin ______°
उत्तर
cos 40° = sin 50°
Explanation:
cos 40° = sin (90° - 40°) = sin 50° ...[cosθ = sin (90° - θ)]
APPEARS IN
संबंधित प्रश्न
In ΔPQR, right angled at Q, PQ = 4 cm and RQ = 3 cm. Find the values of sin P, sin R, sec P and sec R.
if `sec A = 5/4` verify that `(3 sin A - 4 sin^3 A)/(4 cos^3 A - 3 cos A) = (3 tan A - tan^3 A)/(1- 3 tan^2 A)`
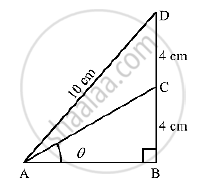
In the adjoining figure, `∠B = 90° , ∠BAC = theta° , BC = CD = 4cm and AD = 10 cm`. find (i) sin theta and (ii) `costheta`
In the adjoining figure, ΔABC is a right-angled triangle in which ∠B = 900, ∠300 and AC = 20cm. Find (i) BC, (ii) AB.
Given: sec A = `( 29 )/(21), "evaluate : sin A" - 1/tan "A"`
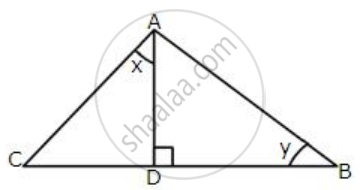
In the following figure:
AD ⊥ BC, AC = 26 CD = 10, BC = 42, ∠DAC = x and ∠B = y.
Find the value of :
(i) cot x
(ii) `1/sin^2 y – 1/tan^2 y`
(iii) `6/cos x – 5/cos y + 8 tan y`.
If sec A = `sqrt2` , find : `(3cot^2 "A"+ 2 sin^2 "A")/ (tan^2 "A" – cos ^2 "A")`.
In ΔABC, ∠A = 90°. If AB = 5 units and AC = 12 units, find: cos C
If sinA = `(3)/(5)`, find cosA and tanA.
If cos A = `3/5`, then find the value of `(sin"A" - cos"A")/(2tan"A")`
