Advertisements
Advertisements
प्रश्न
If A = 30° and B = 60°, verify that cos (A + B) = cos A cos B − sin A sin B
उत्तर
Given
`A = 30^@ and B = 60^@`
To verify:
`cos(A + B) = cos A cos B - sinA sin B` ......(2)
Now consider LHS of the expression to be verified in equation (2)
Therefore,
`cos(30 + 60) = cos 90`
= 0
Now consider RHS of the expression to be verified in equation (2)
Therefore,
cosA cos B - sin A sin B = cos 30 cos 60 - sin 30 sin 60
`= sqrt3/2 xx 1/2 - 1/2 xx sqrt3/2`
= 0
Hence it is verfified that
cos (A + B) = cos A cos B - sin A sin B
APPEARS IN
संबंधित प्रश्न
If Sin (A + B) = 1 and cos (A – B) = 1, 0° < A + B ≤ 90° A ≥ B. Find A & B
In right angled triangle ΔABC at B, ∠A = ∠C. Find the values of sin A sin B + cos A cos B
If cot θ = `3/4` , show that `sqrt("sec θ - cosecθ"/"secθ + cosecθ" ) = 1/ sqrt(7)`
If sec `theta = 17/8 ` verify that `((3-4sin^2theta)/(4 cos^2theta -3))=((3-tan^2theta)/(1-tan^2theta))`
Evaluate:
`4/(cot^2 30^0) +1/(sin^2 30^0) -2 cos^2 45^0 - sin^2 0^0`
Verify each of the following:
(iii) `2 sin 30^0 cos 30^0`
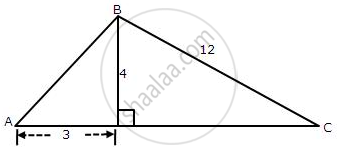
From the following figure, find the values of
(i) cos A
(ii) cosec A
(iii) tan2A - sec2A
(iv) sin C
(v) sec C
(vi) cot2 C - ` 1 / sin^2 "c"`
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
cos A = `(7)/(25)`
From the given figure, find the values of cosec C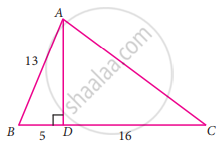
If 2 cos θ = `sqrt(3)`, then find all the trigonometric ratios of angle θ
