Advertisements
Advertisements
प्रश्न
In the diagram, given below, triangle ABC is right-angled at B and BD is perpendicular to AC.
Find:
(i) cos ∠DBC
(ii) cot ∠DBA

उत्तर १
Consider the given figure :
Since the triangle is a right-angled triangle, so using Pythagorean Theorem
AC2 = 52 + 122
AC2 = 25 + 144 + 169
AC = 13
In ΔCBD and ΔCBA, the ∠C is common to both the triangles, ∠CDB = ∠CBA = 90° so therefore ∠CBD = ∠CAB.
Therefore ΔCBD and ΔCBA are similar triangles according to AAA Rule
So
`"AC"/"BC" = "AB"/"BD"`
`(13)/(5) = ( 12)/"BD"`
`"BD = (60)/(13)`
(i) cos ∠DBC = `"base"/"hypotenuse" = "BD"/"BC" = (60/13)/(5) =(12)/(13)`
(ii) cot ∠DBA =`"base"/"perpendicular" = "BD"/"AB" = (60/13)/(12) =(5)/(13)`
उत्तर २
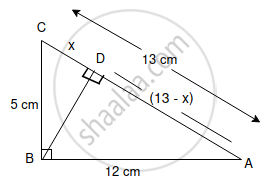
Since the triangle ABC is a right-angled triangle, so using Pythagorean Theorem,
AC2 = BC2 + AB2
AC2 = 52 + 122
AC2 = 25 + 144
AC2 = 169
AC2 = `sqrt169`
AC = 13
In ΔDBC, using Pythagorean Theorem,
BC2 = CD2 + BD2
(5)2 = x2 + BD2
25 - x2 = BD2
BD2 = 25 - x2 ...(i)
In ΔDBA, using Pythagorean Theorem,
BA2 = DA2 + BD2
(12)2 = (13 - x)2 + BD2
144 = (13 - x)2 + BD2
144 = 169 + x2 - 26x + BD2
144 - 169 - x2 + 26x = BD2
BD2 = - 25 - x2 + 26x ...(ii)
From equation (i) and (ii)
25 - x2 = - 25 - x2 + 26x
25 + 25 = 26x
x = `50/26`
x = `25/13`
In ΔBDC,
BC = 5 ; CD = `25/13`
BD2 = 25 - x2
= 25 - `(25/13)^2`
= 25 - `625/169`
= 25 `(1 - 25/169)`
= `25 ((169 - 25)/169)`
BD = `sqrt(25 (144/169))`
BD = `(5 xx 12)/13`
BD = `60/13`
In ΔDBA,
AB = 12; BD = `60/13`
AD = 13 - x
= `13 - 25/13 = (169 - 25)/13 = 144/13`
(i) cos ∠DBC = `"Base"/"hypotenuse" = (60/13)/5 = 60/65 = 12/13`
(ii) cot ∠DBA `= "Base"/"perpendicular" = (60/13)/(144/13) = 60/144 = 10/24 " i.e.," 5/13`
APPEARS IN
संबंधित प्रश्न
In Fig below, Find tan P and cot R. Is tan P = cot R?

In ∆PQR, right-angled at Q, PQ = 3 cm and PR = 6 cm. Determine ∠P and ∠R.
In a ΔABC , ∠B = 90° , AB= 24 cm and BC = 7 cm find (i) sin A (ii) cos A (iii) sin C (iv) cos C
Evaluate:
`cot^2 30^0-2cos^2 30^0-3/4 sec^2 45^0 +1/4 cosec^2 30^0`
Using the formula, sin A = `sqrt((1-cos 2A)/2) ` find the value of sin 300, it being given that cos 600 = `1/2`
In triangle ABC, AB = AC = 15 cm and BC = 18 cm, find cos ∠ABC.
In the given figure;
BC = 15 cm and sin B = `(4)/(5)`
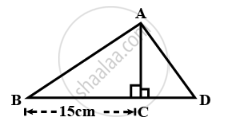
- Calculate the measure of AB and AC.
- Now, if tan ∠ADC = 1; calculate the measures of CD and AD.
Also, show that: tan2B - `1/cos^2 "B" = – 1 .`
In triangle ABC, ∠B = 90° and tan A = 0.75. If AC = 30 cm, find the lengths of AB and BC.
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
sinB = `sqrt(3)/(2)`
If 8 tanθ = 15, find (i) sinθ, (ii) cotθ, (iii) sin2θ - cot2θ
