Advertisements
Advertisements
Question
In right angled triangle ABC. ∠C = 90°, ∠B = 60°. AB = 15 units. Find remaining angles and sides.
Solution 1
We are given the following triangle with related information
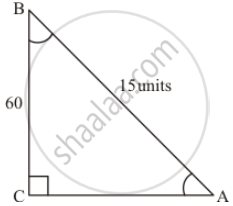
It is required to find ∠A, ∠C and length of sides AC and BC
ΔABC is right angled at C
Therefore,
`∠C = 90^@`
Now we know that sum of all the angles of any triangle is `180^@`
Therefore
`∠A + ∠B + ∠C = 180^@`
Now by substituting the values of known angles and in equation (1)
We get,
`∠A + 60^@ + 90^2 = 180^@`
Therefore
`∠A + 150^@ = 180^@`
`=> ∠A = 180^@ - 150^@`
`=> ∠A = 30^@`
Therefore,
`∠A = 30^@`
Now
We know that,
`cos B = cos 60^@`
`=> (BC)/(AB) = cos 60^@`
Now we have,
AB =15 units and `cos 60^@ = 1/2`
Therefore by substituting above values in equation (2)
We get,
`cos B = cos 60^@`
`=> (BC)/(AB) = cos 60^@`
`=> (BC)/15 = 1/2`
Now by cross multiplying we get,
`(BC)/15 = 1/2`
`=> 2 xx BC = 15 xx 1`
`=> BC = 15/2`
=> BC = 7.5
Therefore
BC = 7.5 units ....(3)
Now
We know that
`sin B = sin 60^@`
`=> (AC)/(AB) = sin 60^@` .........(4)
Now
We know that,
AB=15 units and
Solution 2
We are given the following triangle with related information

It is required to find ∠A, ∠C and length of sides AC and BC
ΔABC is right angled at C
Therefore,
`∠C = 90^@`
Now we know that sum of all the angles of any triangle is `180^@`
Therefore
`∠A + ∠B + ∠C = 180^@`
Now by substituting the values of known angles and in equation (1)
We get,
`∠A + 60^@ + 90^2 = 180^@`
Therefore
`∠A + 150^@ = 180^@`
`=> ∠A = 180^@ - 150^@`
`=> ∠A = 30^@`
Therefore,
`∠A = 30^@`
Now
We know that,
`cos B = cos 60^@`
`=> (BC)/(AB) = cos 60^@`
Now we have,
AB =15 units and `cos 60^@ = 1/2`
Therefore by substituting above values in equation (2)
We get,
`cos B = cos 60^@`
`=> (BC)/(AB) = cos 60^@`
`=> (BC)/15 = 1/2`
Now by cross multiplying we get,
`(BC)/15 = 1/2`
`=> 2 xx BC = 15 xx 1`
`=> BC = 15/2`
=> BC = 7.5
Therefore
BC = 7.5 units ....(3)
Now
We know that
`sin B = sin 60^@`
`=> (AC)/(AB) = sin 60^@` .........(4)
Now
We know that,
`AB=15 units and sin 60^@ = sqrt3/2`
Therefore by substituting above values in equation (4)
We get,
`sin B = sin 60^@`
`=> (AC)/(AB) = sin 60^@`
`=> (AC)/15 = sqrt3/2`
Now by cross multiplying we get,
`=> 2 xx AC = sqrt3 xx 15`
`=> AC = (sqrt3 x 15)/2`
`=> AC = 15/2 sqrt3`
Therefore,
AC = 15/2 sqrt3` units`
Hence
`A = 30^@`
`BC = 7.5untis`
`AC = 15/2 sqrt3` units
APPEARS IN
RELATED QUESTIONS
If cot θ = 2 find all the values of all T-ratios of θ .
If tan `theta = a/b`, show that `((a sin theta - b cos theta))/((a sin theta + bcos theta))= ((a^2-b^2))/(a^2+b^2)`
Evaluate:
`(5 cos^2 60^circ + 4 sec^2 30^circ - tan^2 45^circ)/(sin^2 30^circ + cos^2 30^circ)`
If A = 600 and B = 300, verify that:
(i) sin (A – B) = sin A cos B – cos A sin B
If sin (A+B) = sin A cos B + cos A sin B and cos (A-B) = cos A cos B + sin A sin B
(i) sin (750)
(ii) cos (150)
Given: cos A = `( 5 )/ ( 13 )`
Evaluate:
- `(sin "A "–cot "A") / (2 tan "A")`
- `cot "A" + 1/cos"A"`
If sec A = `sqrt2`, find the value of :
`(3cos^2"A"+5tan^2"A")/(4tan^4"A"–sin^2"A")`
In the diagram, given below, triangle ABC is right-angled at B and BD is perpendicular to AC.
Find:
(i) cos ∠DBC
(ii) cot ∠DBA

In the given figure; ∠C = 90o and D is mid-point of AC.
Find :
(i) `(tan∠CAB)/ (tan∠CDB)` (ii) `(tan∠ABC)/ (tan∠DBC)`
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
cosB = `(4)/(5)`
