Advertisements
Advertisements
Question
If cosec θ = `sqrt5`, find the value of:
- 2 - sin2 θ - cos2 θ
- 2 + `1/sin^2"θ" – cos^2"θ"/sin^2"θ"`
Solution
Consider the diagram below :

cosec θ =`sqrt5`
i.e.`"hypotenuse"/"perpendicular" = sqrt5/1`
Therefore, if length of hypotenuse = `sqrt5`, length of perpendicular = x
Since
base2 + perpendicular2 = hypotenuse2 ...[Using Pythagoras Theorem]
base2 + (x)2 = `(sqrt5x)^2`
base2 = 5x2 – x2
base2 = 4x2
∴ base = 2x
Now
sin θ = `"perpendicular"/"hypotenuse" = (x)/(sqrt5x) = (1)/(sqrt5)`
cos θ = `"base"/"hypotenuse" = (2)/(sqrt5x) = (2)/(sqrt5)`
(i) 2 – sin2 θ – cos2 θ
= 2 – `(1/sqrt5)^2 – (2/sqrt5)^2`
= 2 – `(1)/(5) –(4)/(5)`
= `(5)/(5)`
= 1
(ii) 2 + `1/sin^2"θ" – cos^2"θ"/sin^2"θ"`
= 2 + `1/(x/sqrt(5x))^2 – ((2x)/(sqrt5x))^2/(x/(sqrt5)^2)`
= `2 + 5 – (4/5)/(1/5)`
= 2 + 5 – 4
= 7 – 4
= 3
APPEARS IN
RELATED QUESTIONS
In ΔPQR, right angled at Q, PQ = 4 cm and RQ = 3 cm. Find the values of sin P, sin R, sec P and sec R.
If cos 2θ = sin 4θ where 2θ, 4θ are acute angles, find the value of θ.
If tan θ =`15/ 8 `, find the values of all T-ratios of θ.
If sin ∝ = `1/2` prove that (3cos∝ - `4cos^2` ∝)=0
If a right ΔABC , right-angled at B, if tan A=1 then verify that 2sin A . cos A = 1
sin20° = cos ______°
Given: tan A = `4/3 , "find" : ("cosec""A")/(cot "A"– sec "A")`
In the figure given below, ABC is an isosceles triangle with BC = 8 cm and AB = AC = 5 cm. Find:
(i) sin B
(ii) tan C
(iii) sin2 B + cos2B
(iv) tan C - cot B
Using the measurements given in the following figure:
(i) Find the value of sin θ and tan θ.
(ii) Write an expression for AD in terms of θ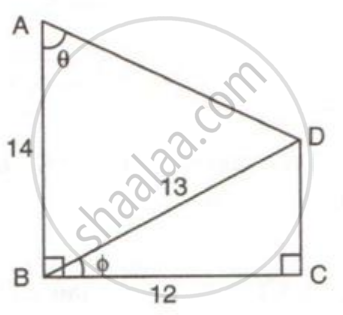
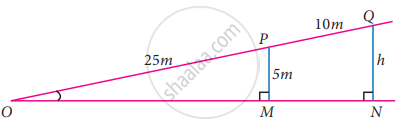
A boy standing at a point O finds his kite flying at a point P with distance OP = 25 m. It is at a height of 5 m from the ground. When the thread is extended by 10 m from P, it reaches a point Q. What will be the height QN of the kite from the ground? (use trigonometric ratios)