If Tan a + Cot a = 5; Find the Value of Tan2 A + Cot2 A - Mathematics

If tan A + cot A = 5;
Find the value of tan² A + cot² A.

Sum

tan A+cotA = 5
Squaring both sides

(tan A +cotA)² = 5²
tan² A+ cot² A+2 tan A. cotA = 25
tan² A+cot² A+2 tan A. `1/ tan "A"` = 25
tan² A+cot² A = 23

shaalaa.com

Is there an error in this question or solution?

Chapter 22: Trigonometrical Ratios [Sine, Consine, Tangent of an Angle and their Reciprocals] - Exercise 22 (B) [Page 286]

Chapter 22 Trigonometrical Ratios [Sine, Consine, Tangent of an Angle and their Reciprocals]
Exercise 22 (B) | Q 11 | Page 286

In right angled triangle ΔABC at B, ∠A = ∠C. Find the values of sin A sin B + cos A cos B

If sec 2A = cosec (A – 42°) where 2A is an acute angle. Find the value of A.

If sec θ = `5/4 ` show that `((sin θ - 2 cos θ))/(( tan θ - cot θ)) = 12/7`

Evaluate:
sin60⁰ cos30⁰ + cos60⁰ sin30⁰

`(cos 28°)/(sin 62°)` = ?

cos 40° = sin ______°

In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.

cosB = `(4)/(5)`

In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: cot²P - cosec²P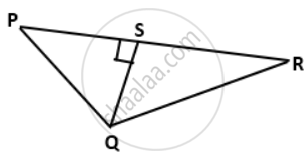

From the given figure, find the values of cosec C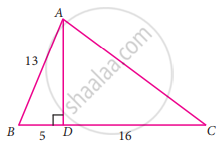

If A + B = 90°, cot B = `3/4` then tan A is equal to ______.