Question

Given: 4 sin θ = 3 cos θ ; find the value of:
(i) sin θ (ii) cos θ
(iii) cot² θ - cosec² θ .
(iv) 4 cos²θ- 3 sin²θ+2

Answer 1

Consider the diagram below :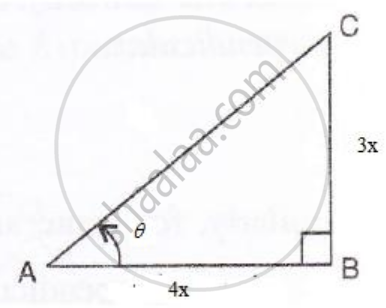

4 sin θ = 3cos θ
tan θ =`(3)/(4)`

i.e.`"perpendicular"/"base"= (3)/(4) ⇒ "BC"/"AB" = (3)/(4)`

Therefore if length of BC = 3x, length of AB = 4x

Since
AB² + BC² = AC²  ... [ Using Pythagoras Theorem]

(4x)² + (3x)² = AC²

AC² = 25x²

∴ AC = 5x          ...( hypotenuse)

(i) sin θ = `"BC"/"AC" = (3)/(5)`

(ii) cos θ = `"AB"/"AC" = (4)/(5)`

(iii) cot θ = `"AB"/"BC" = (4)/(3)`

cosec θ = `"AC"/"BC" = (5)/(3)`

Therefore

cot²θ – cosec²θ

= `(4/3)^2 – (5/3)^2`

= `(16 – 25)/(9)`

= `– (9)/(9)`

= – 1

(iv) 4 cos² θ – 3sin² θ + 2

= `4(4/5)^2 – 3(3/5)^2+2`

= `(64)/(25) – (27)/(25) + 2 `

= `(64 – 27 + 50)/(25)`

= `(87)/(25)`

= `3(12)/(25)`