Advertisements
Advertisements
प्रश्न
If sin (A + B) = 1 and cos (A – B) = 1, 00 ≤ (A + B) ≤ 900 and A > B, then find A and B.
उत्तर
Here, sin (A + B) = 1
⇒ sin (A + B) = 900 [∵ sin 900 = 1]
⇒ (A + B) = 900 …….(i)
Also, cos (A – B) = 1
⇒ cos (A – B) = 00 [∵ cos 00 = 1]
⇒ A – B = 00 ….(ii)
Solving (i) and (ii), we get:
A = 450 and B = 450
APPEARS IN
संबंधित प्रश्न
if `sin theta = 3/5 " evaluate " (cos theta - 1/(tan theta))/(2 cot theta)`
In right angled triangle ΔABC at B, ∠A = ∠C. Find the values of Sin A cos C + Cos A Sin C
If cos 2θ = sin 4θ where 2θ, 4θ are acute angles, find the value of θ.
If tan θ = `4/3`, show that `(sintheta + cos theta )=7/5`
If 3 cot `theta = 2, `show that `((4 sin theta - 4 cos theta))/((2 sin theta + 6 cos theta ))=1/3`
If 3x = cosecθ = and `3/x= cottheta` find the value of 3`(x^2-1/x^2)`.
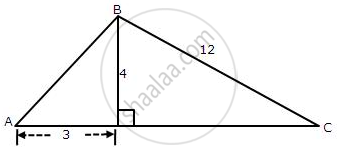
From the following figure, find the values of
(i) cos A
(ii) cosec A
(iii) tan2A - sec2A
(iv) sin C
(v) sec C
(vi) cot2 C - ` 1 / sin^2 "c"`
In rhombus ABCD, diagonals AC and BD intersect each other at point O.
If cosine of angle CAB is 0.6 and OB = 8 cm, find the lengths of the side and the diagonals of the rhombus.
If 3 cot A = 2, then find the value of `(4sin"A" - 3cos"A")/(2sin"A" + 3cos"A")`
Statement A (Assertion): For 0 < θ ≤ 90°, cosec θ – cot θ and cosec θ + cot θ are reciprocal of each other.
Statement R (Reason): cosec2 θ – cot2 θ = 1
